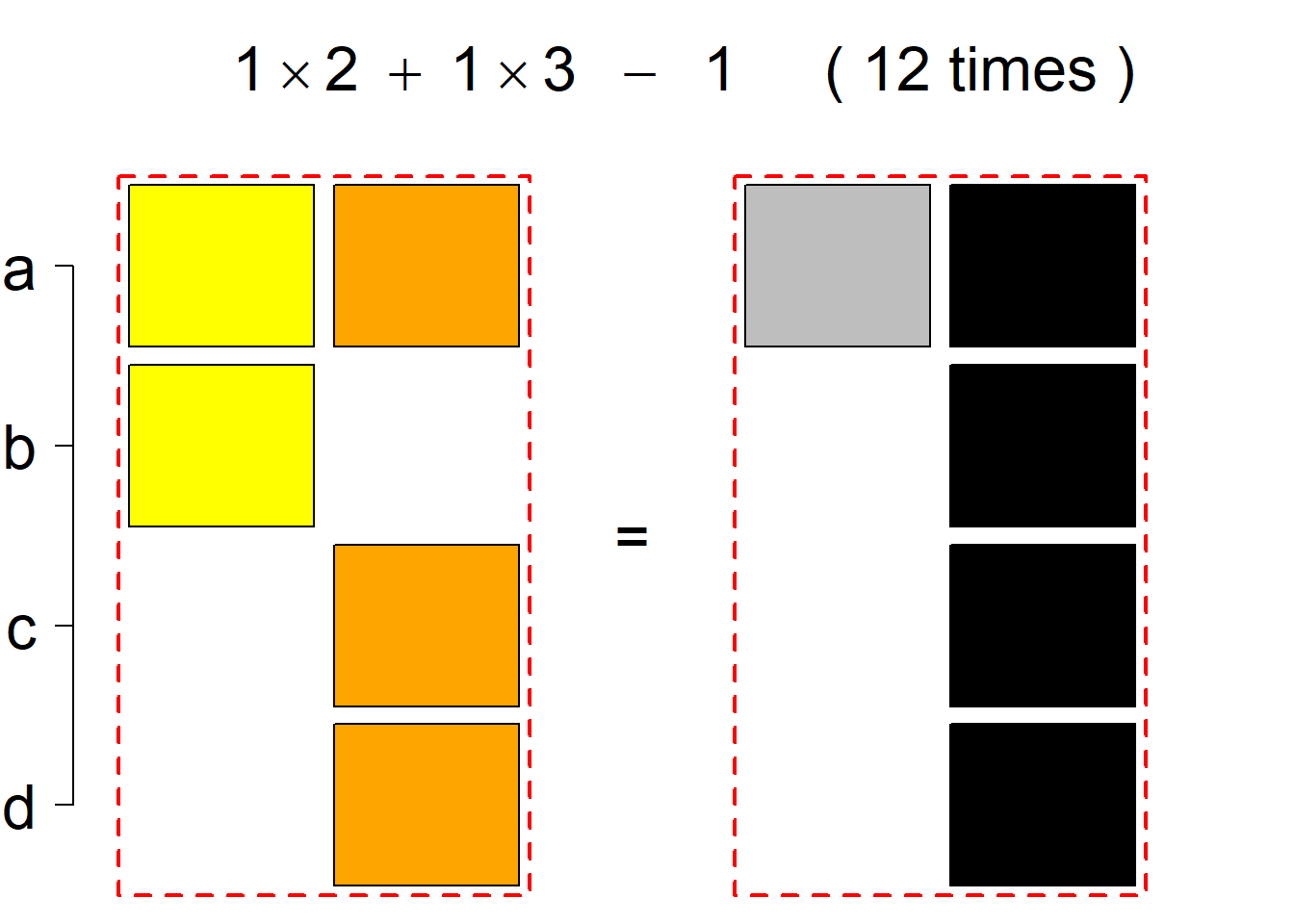
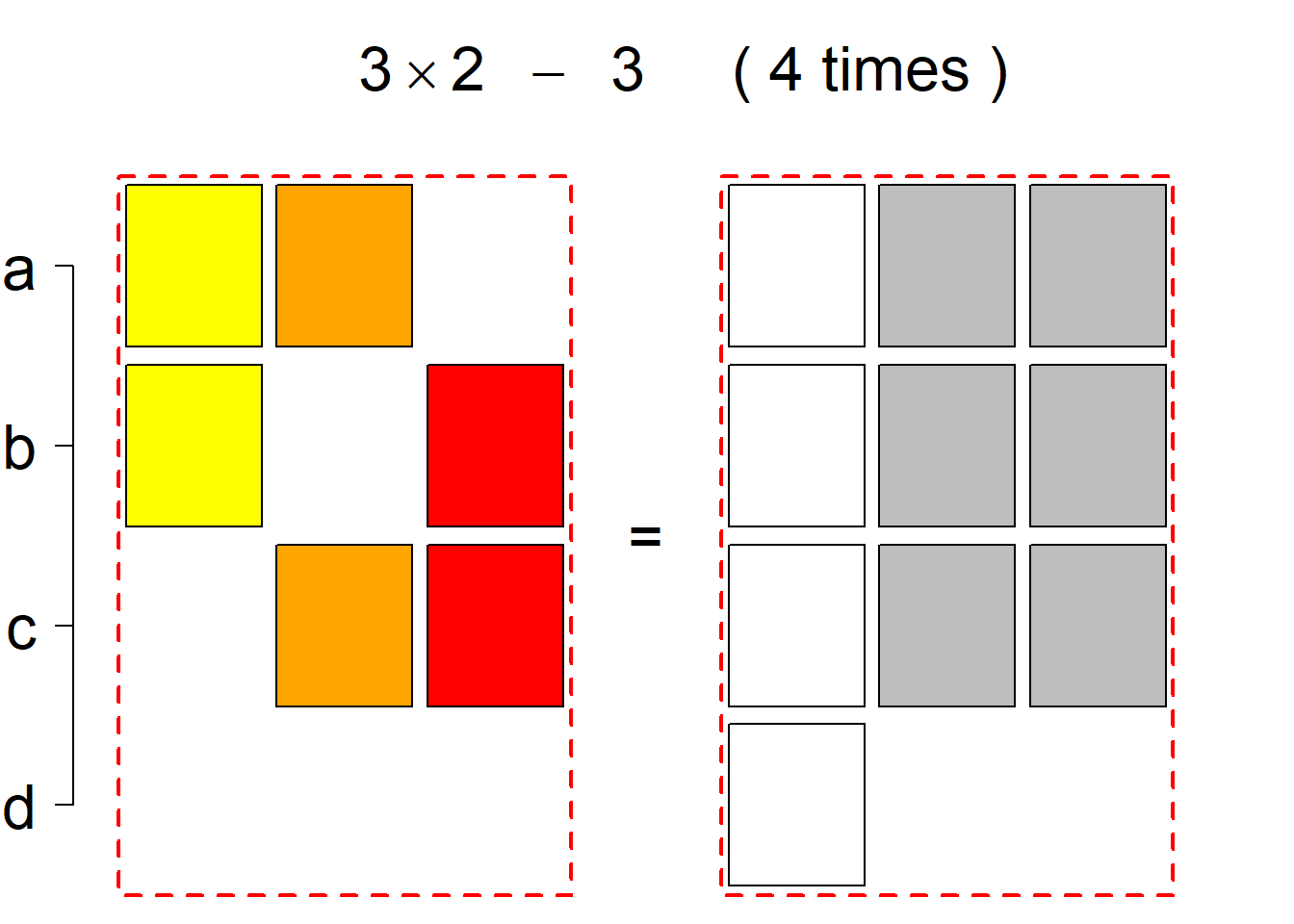
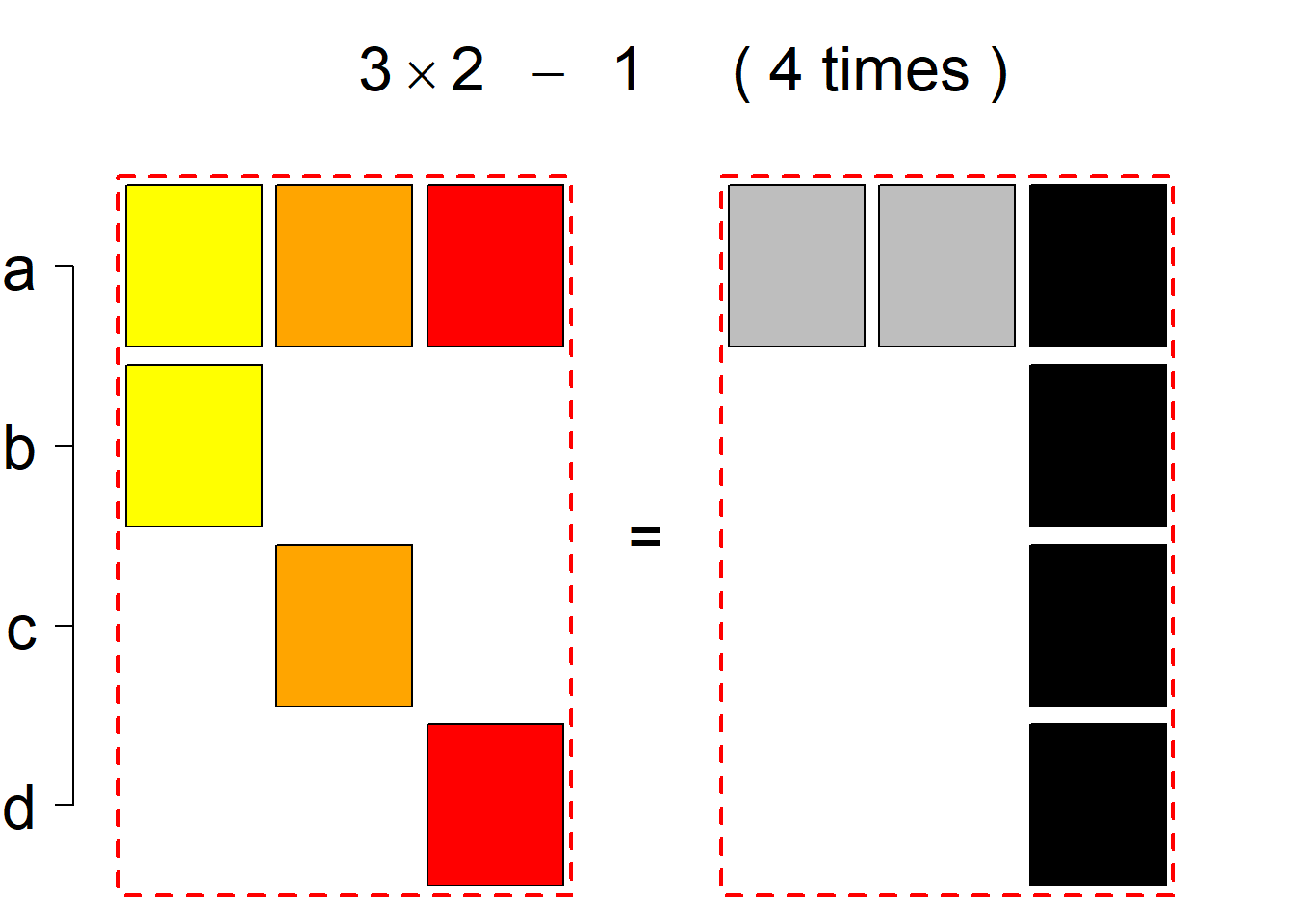
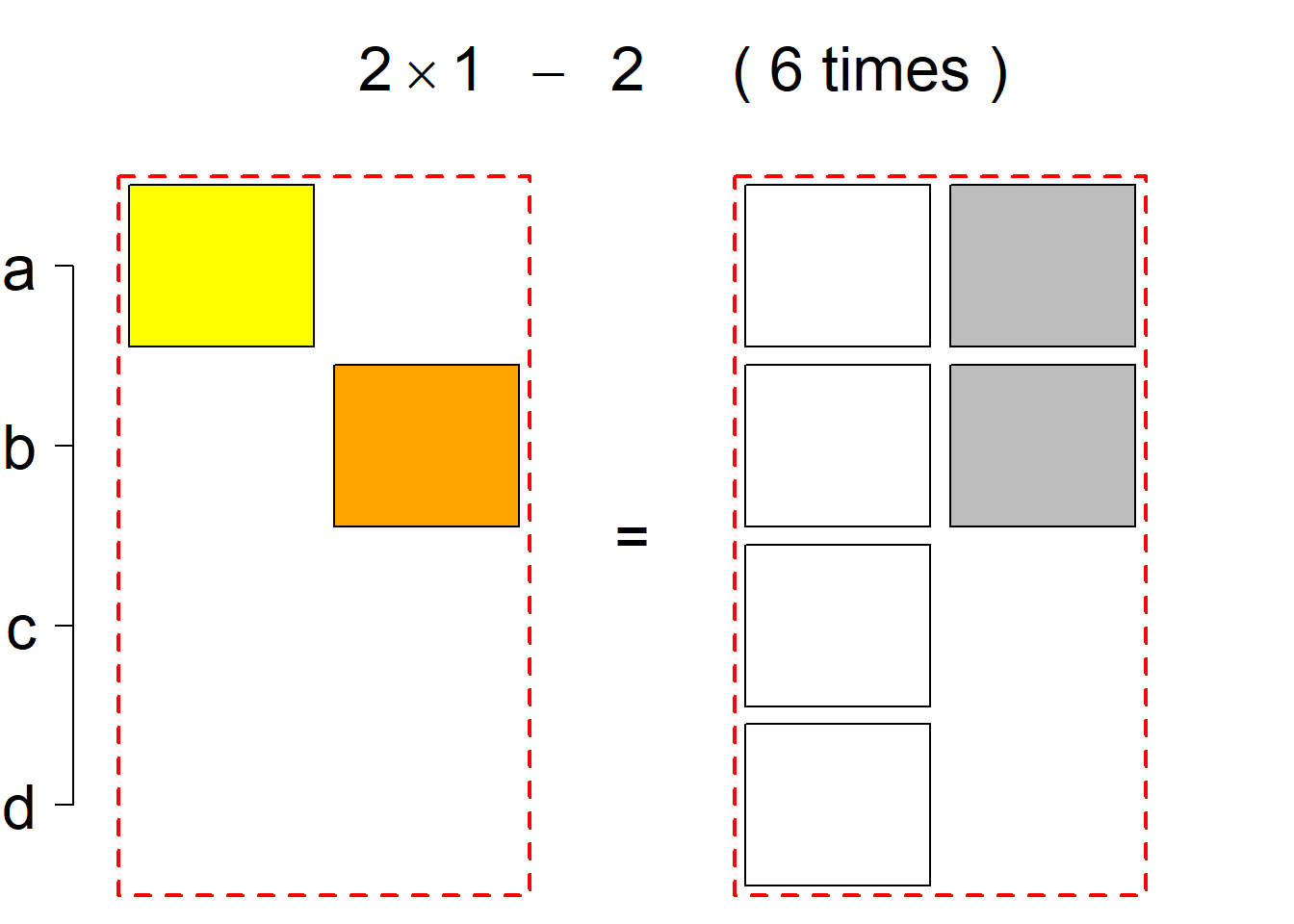|N|=4
Indecomposable min-semi-balanced systems
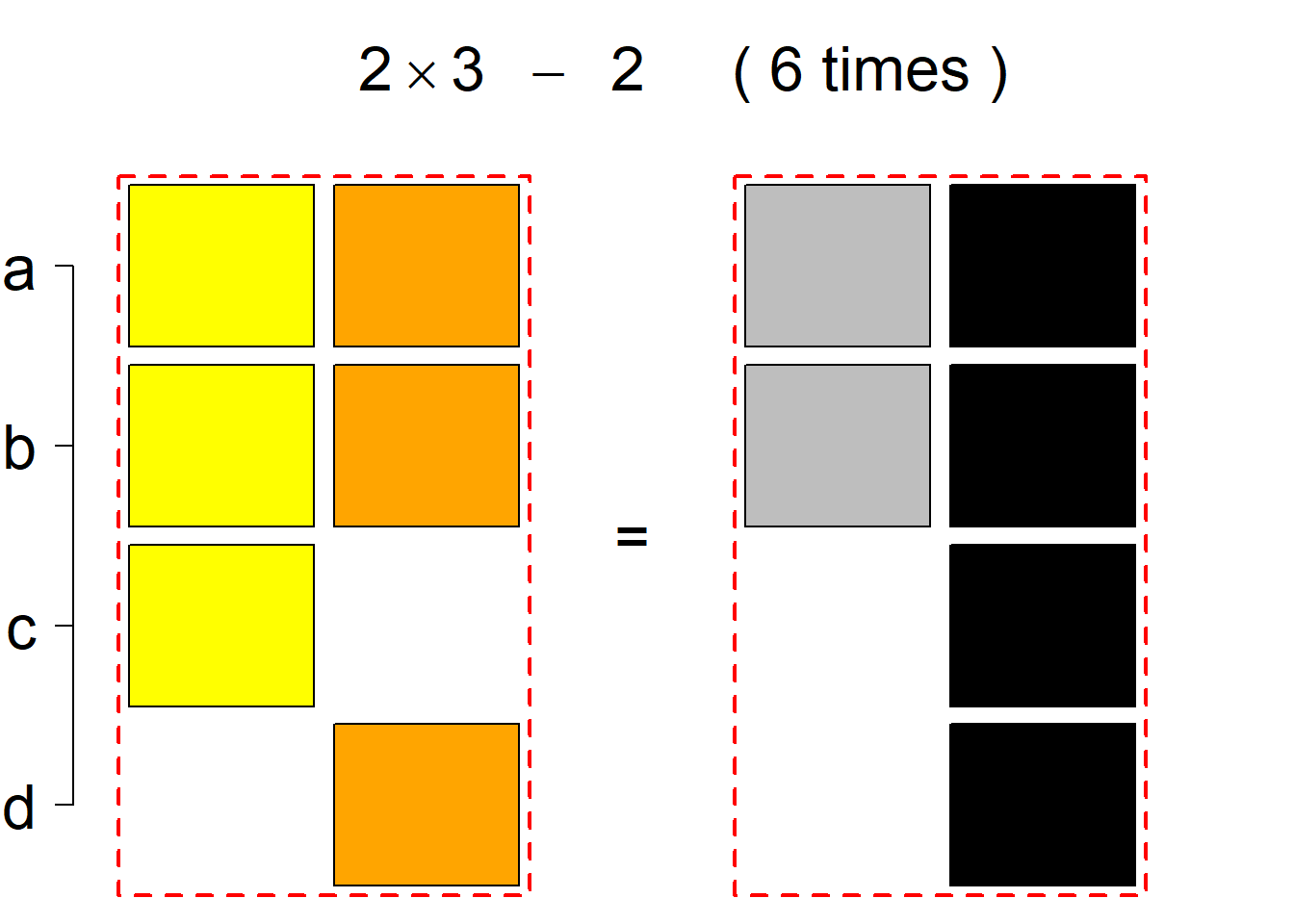
There are 44 such systems breaking into 6 permutational types. Specifically, the first classification class consists of 22 such systems falling into 3 permutational types, the same holds for the (complementary) second classification class, and there is no system belonging to the third classification class.
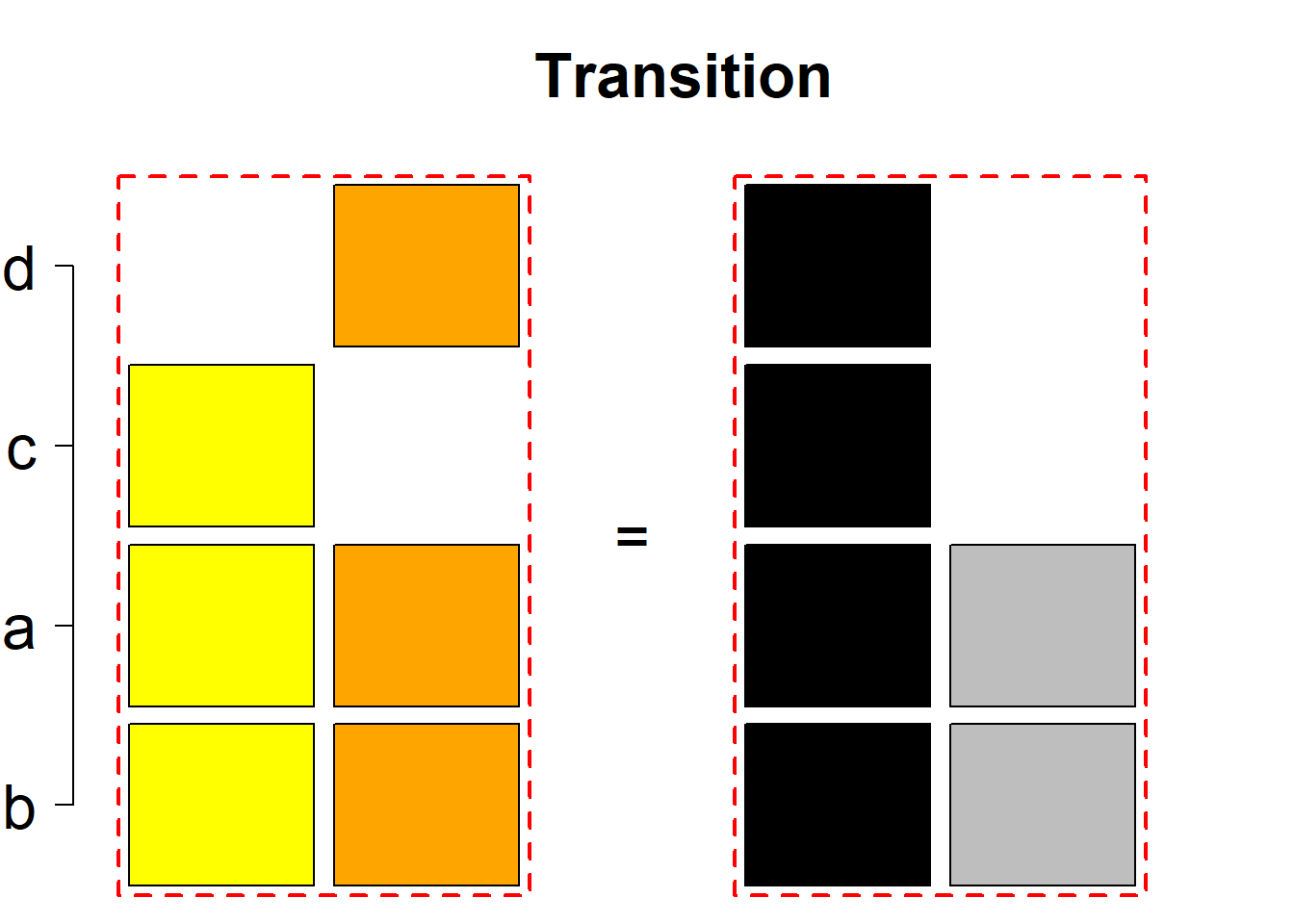
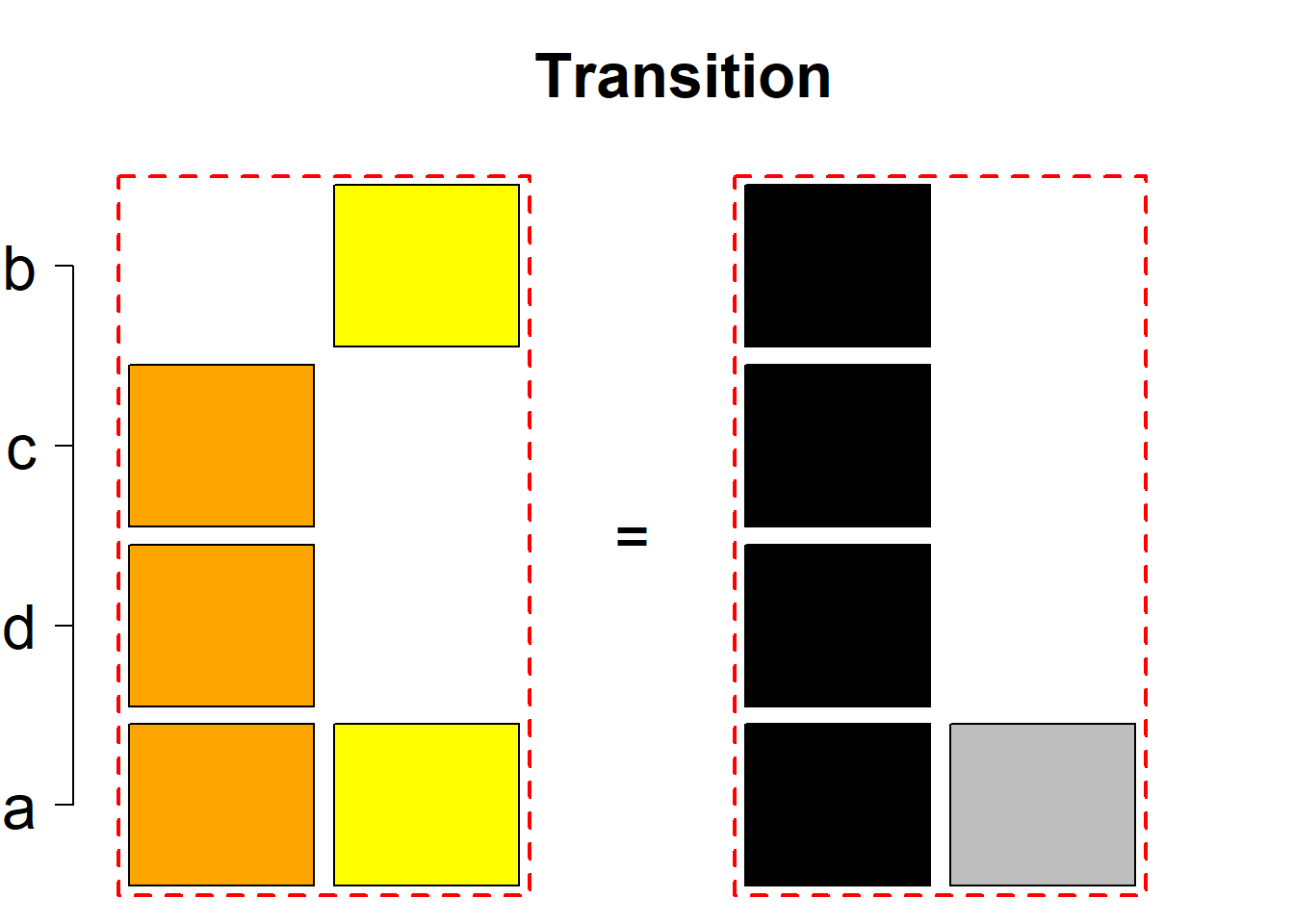
Each permutational type is labeled by a formal arithmetic expression which encodes the cardinalities of involved sets. The number of involved set systems in a permutation type is in the bracket followed. Two mutually complementary permutational types are on the same hyper-row, represented by the left and right diagrams in the hyper-row. The middle diagram in the hyper-row is auxiliary, to describe the transition from the type on the left-hand side to its complementary type on the right-hand side. Specifically, the middle diagram describes just the complementary system to the system in the left diagram, and labels of its rows encode the permutation of variables (= rows) which leads to the set system in the right diagram.