|N|=6
Indecomposable min-semi-balanced systems
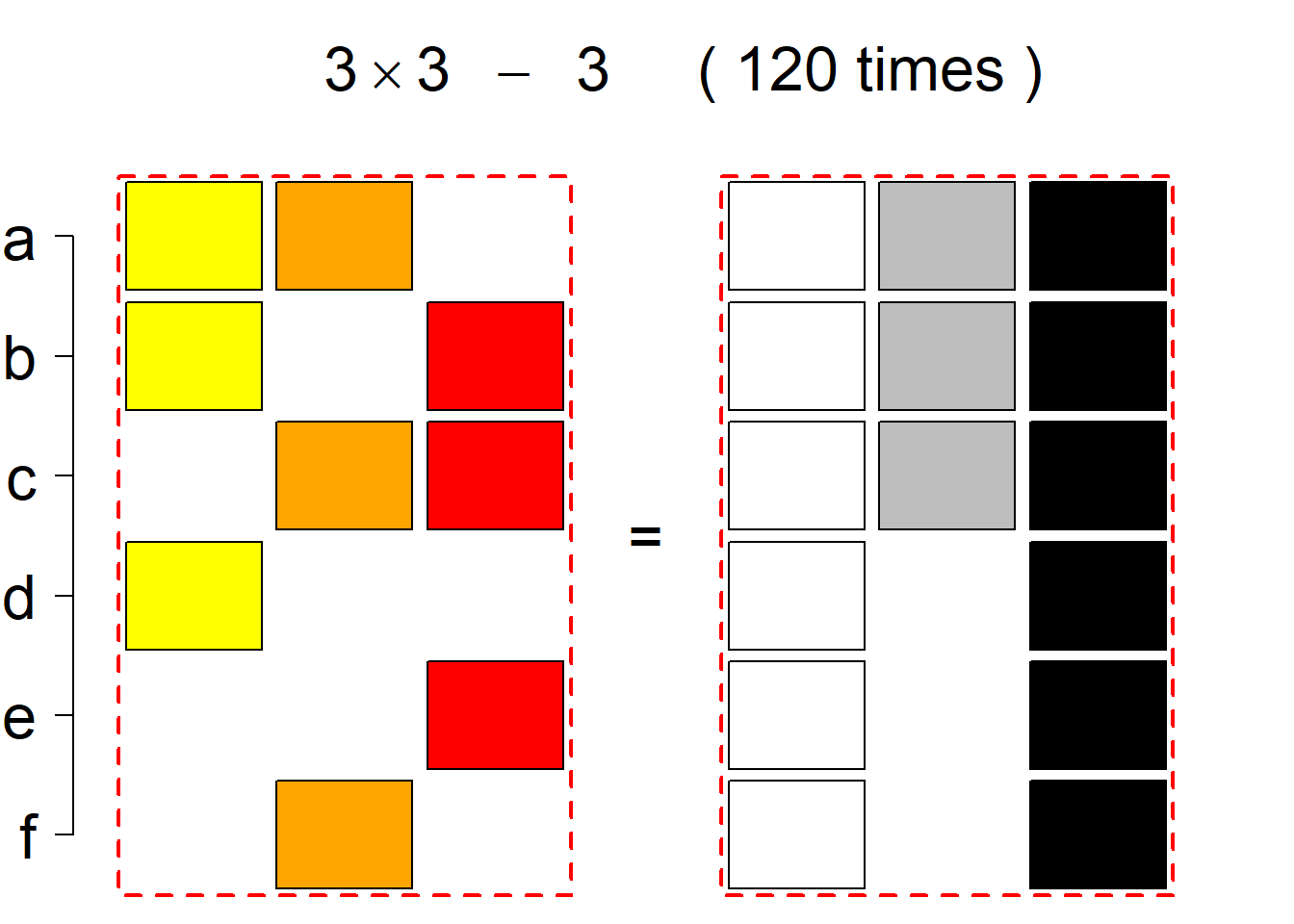
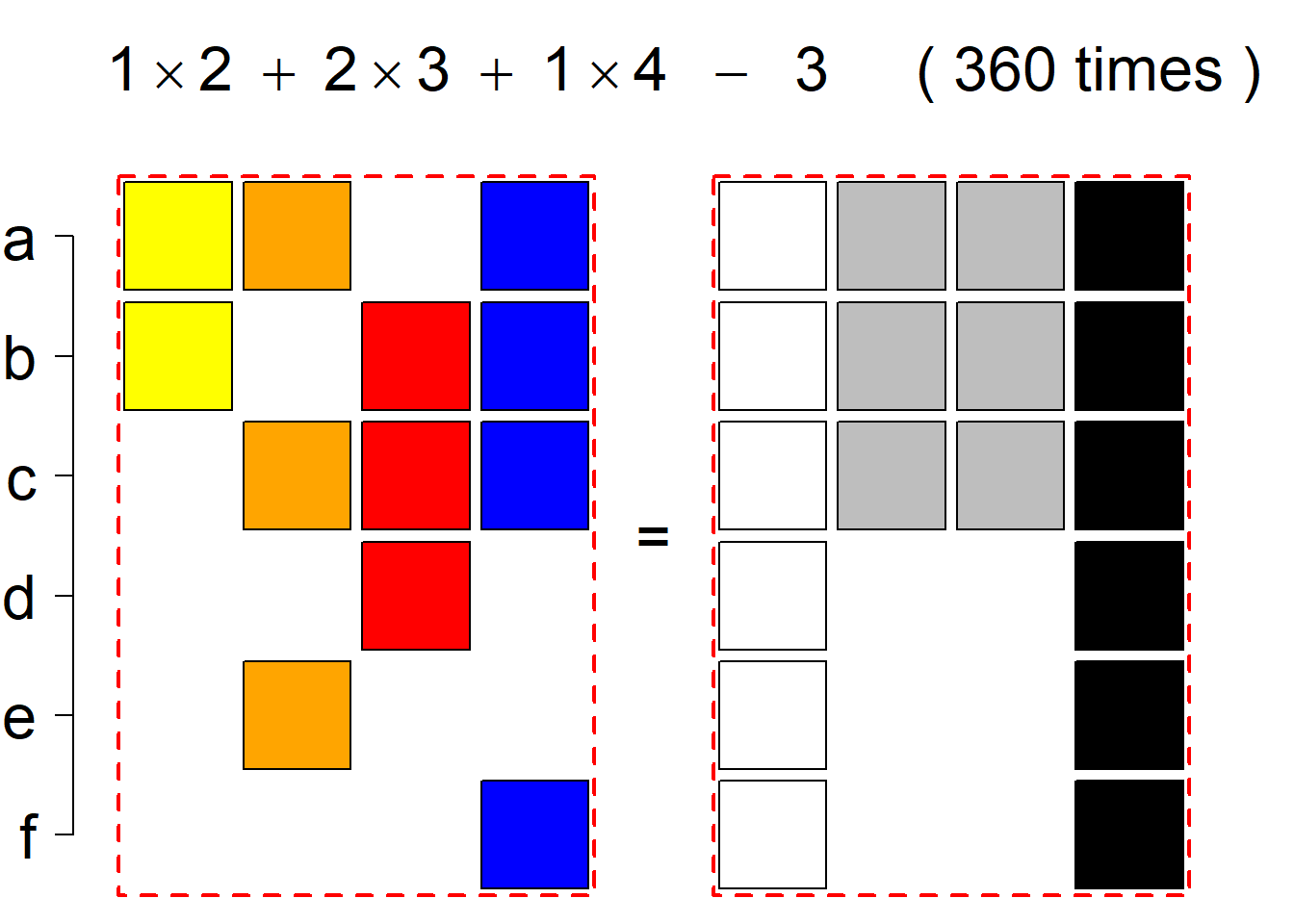
There are 7006 such systems breaking into 53 permutational types. More specifically, the first classification class consists of 2093 such systems falling into 23 permutational types, the same holds for the (complementary) second classification class. The third classification class consists of 2820 such systems falling into 7 permutational types.
The first two classification classes
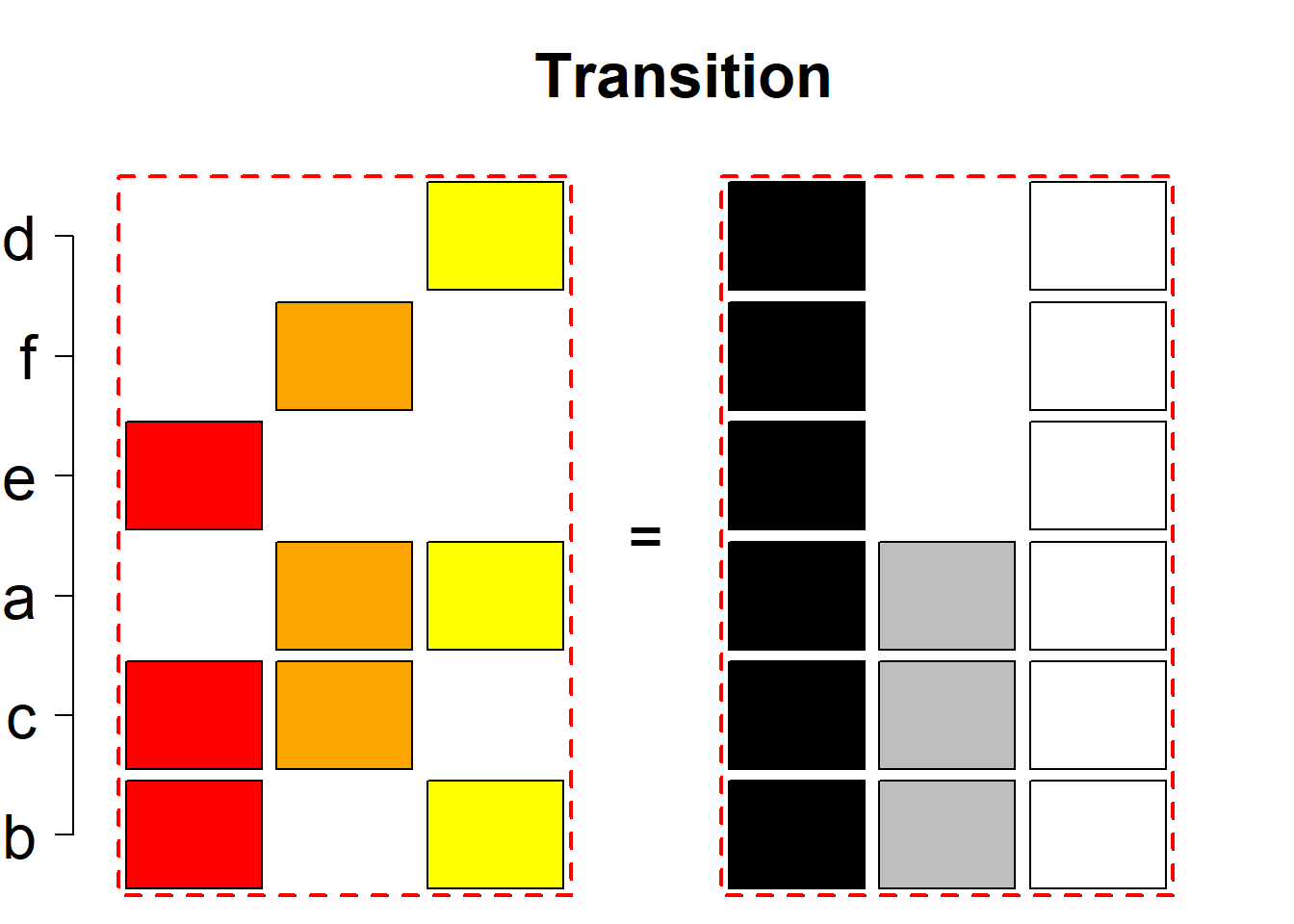
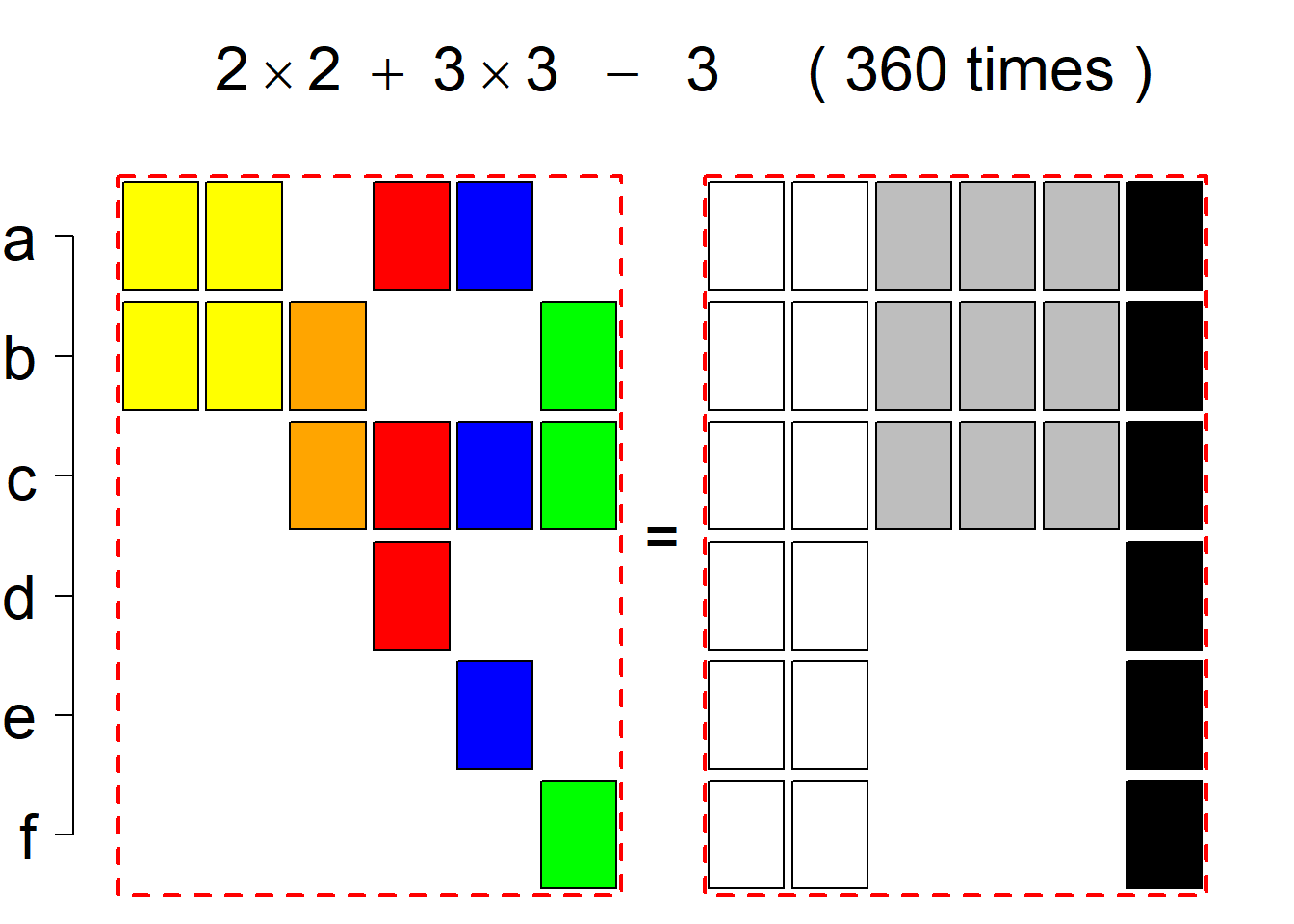
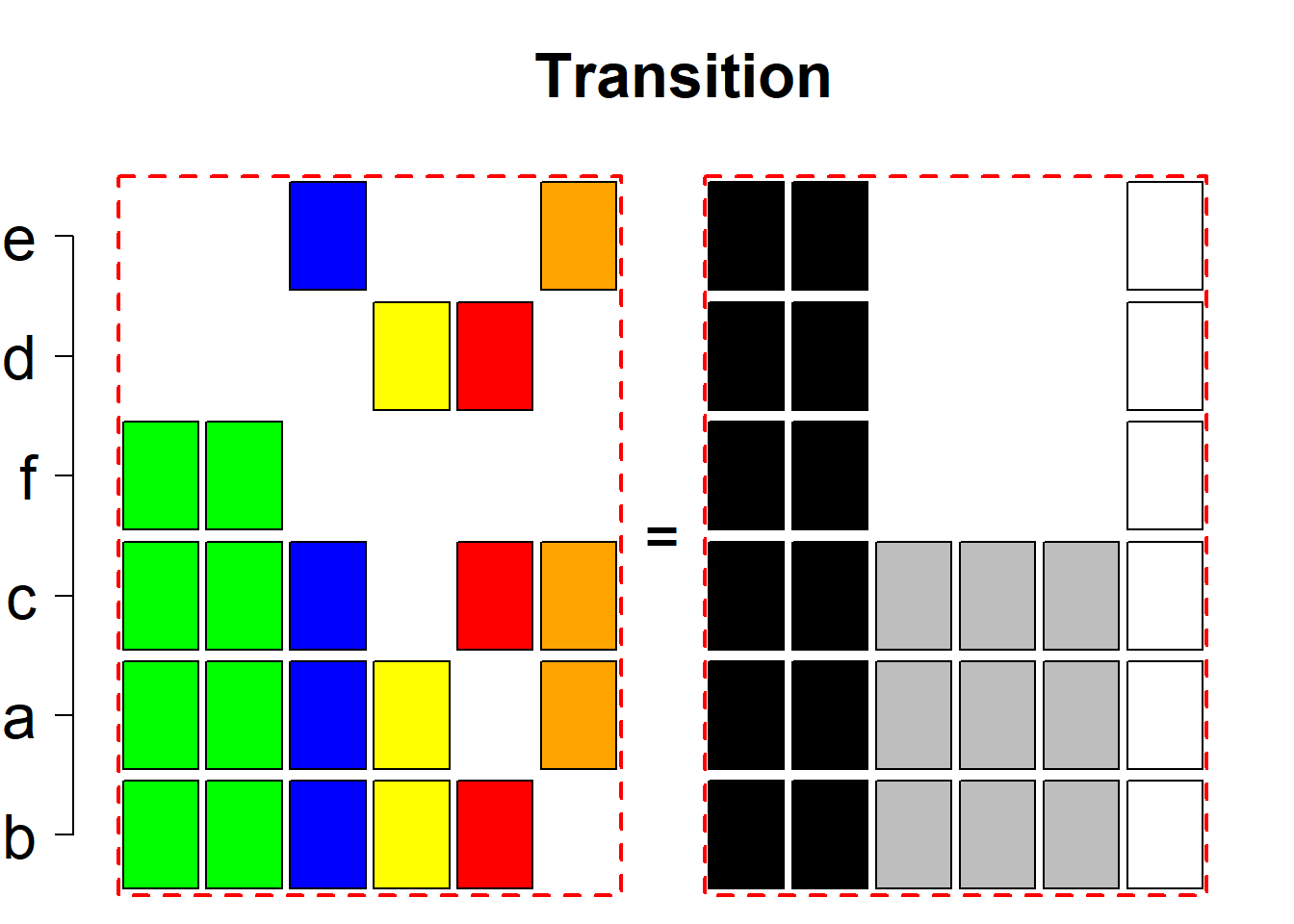
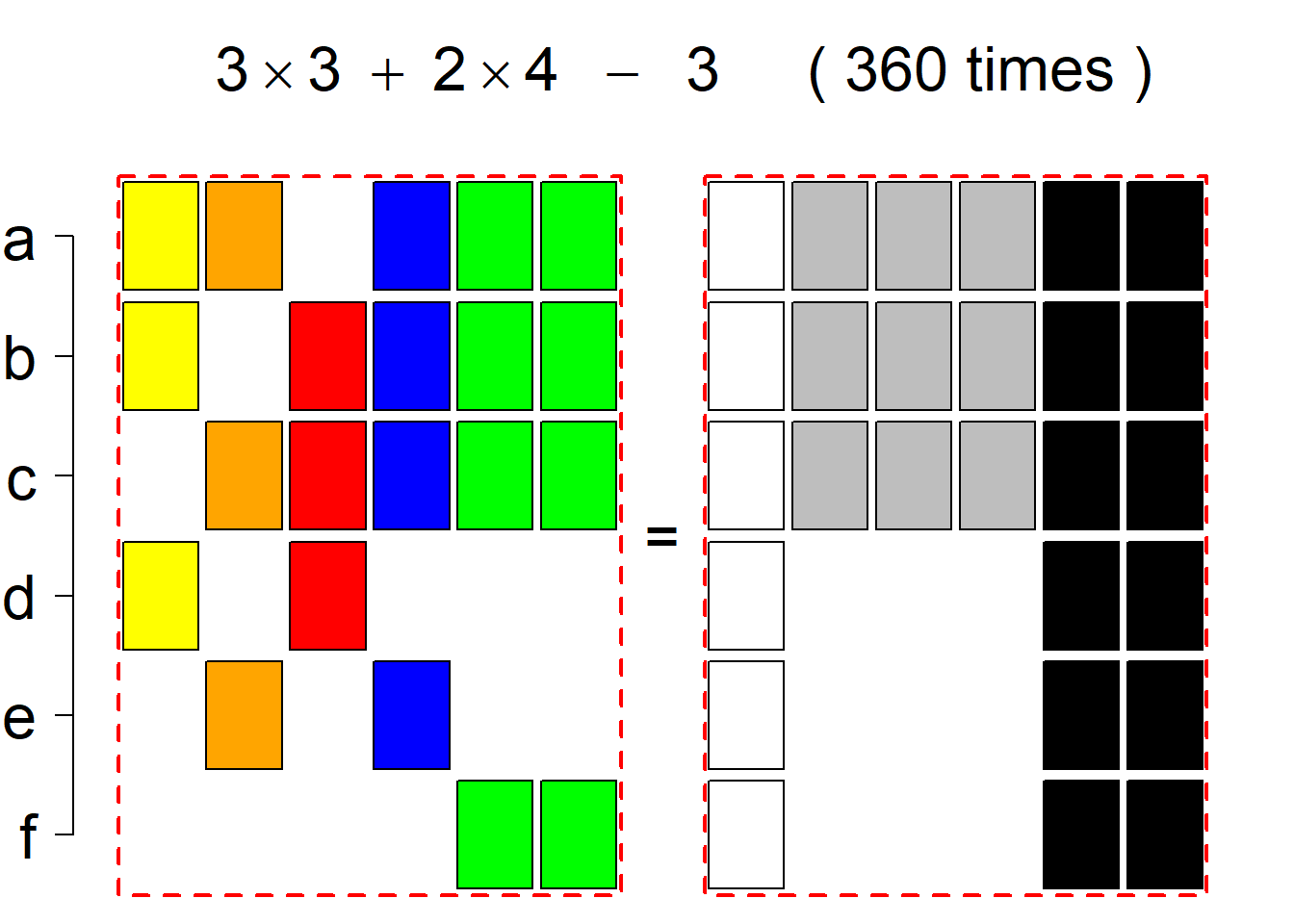
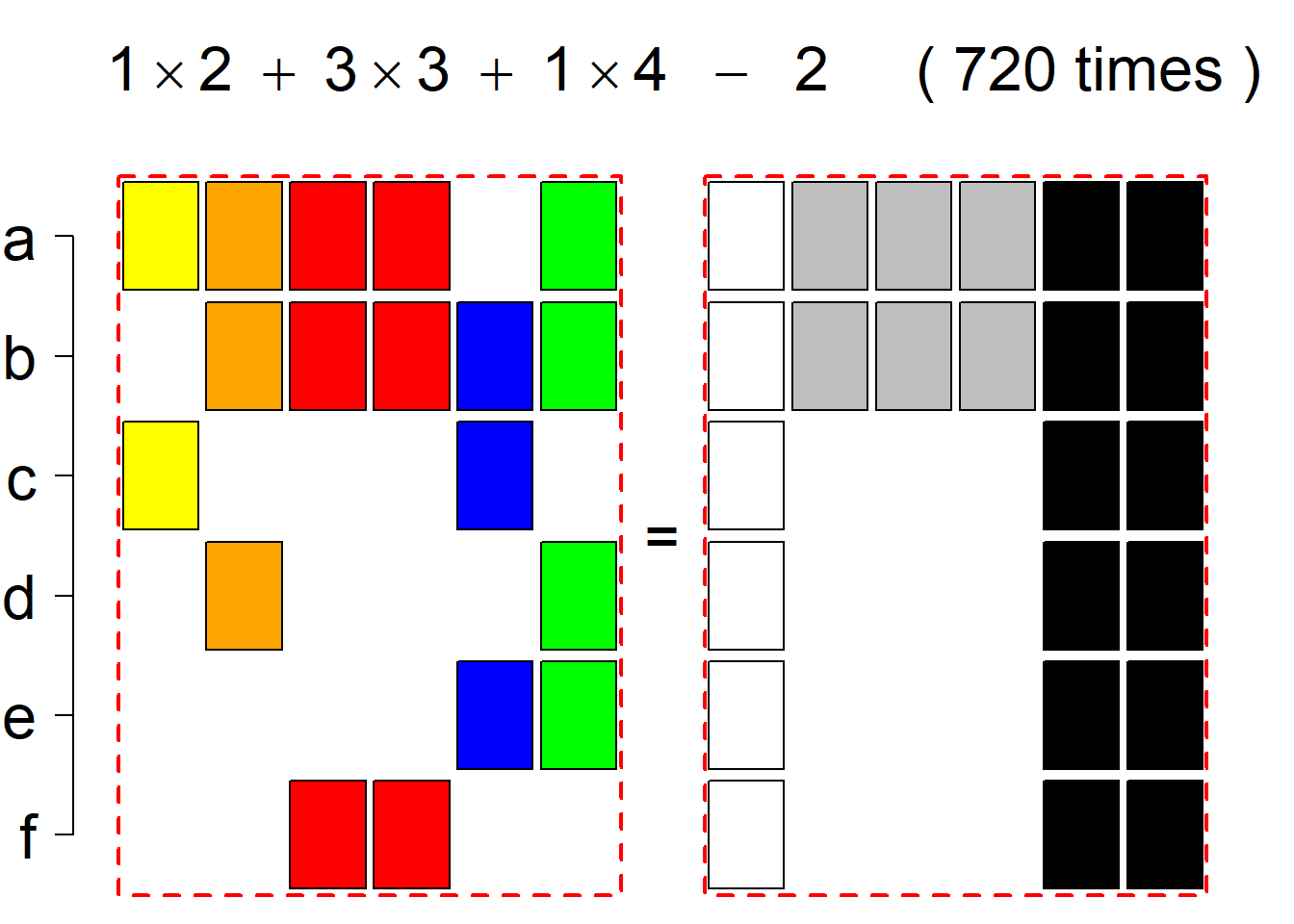
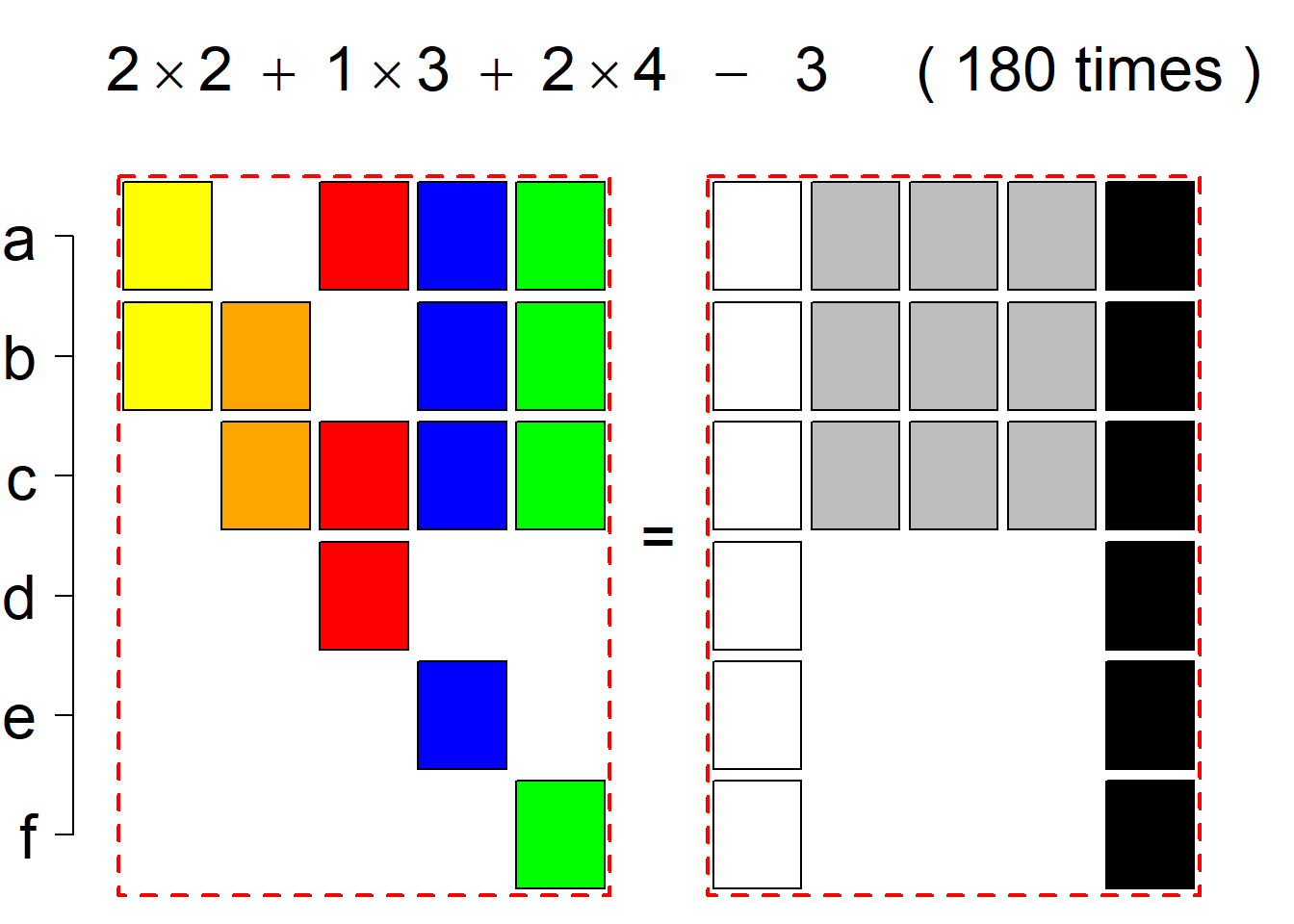
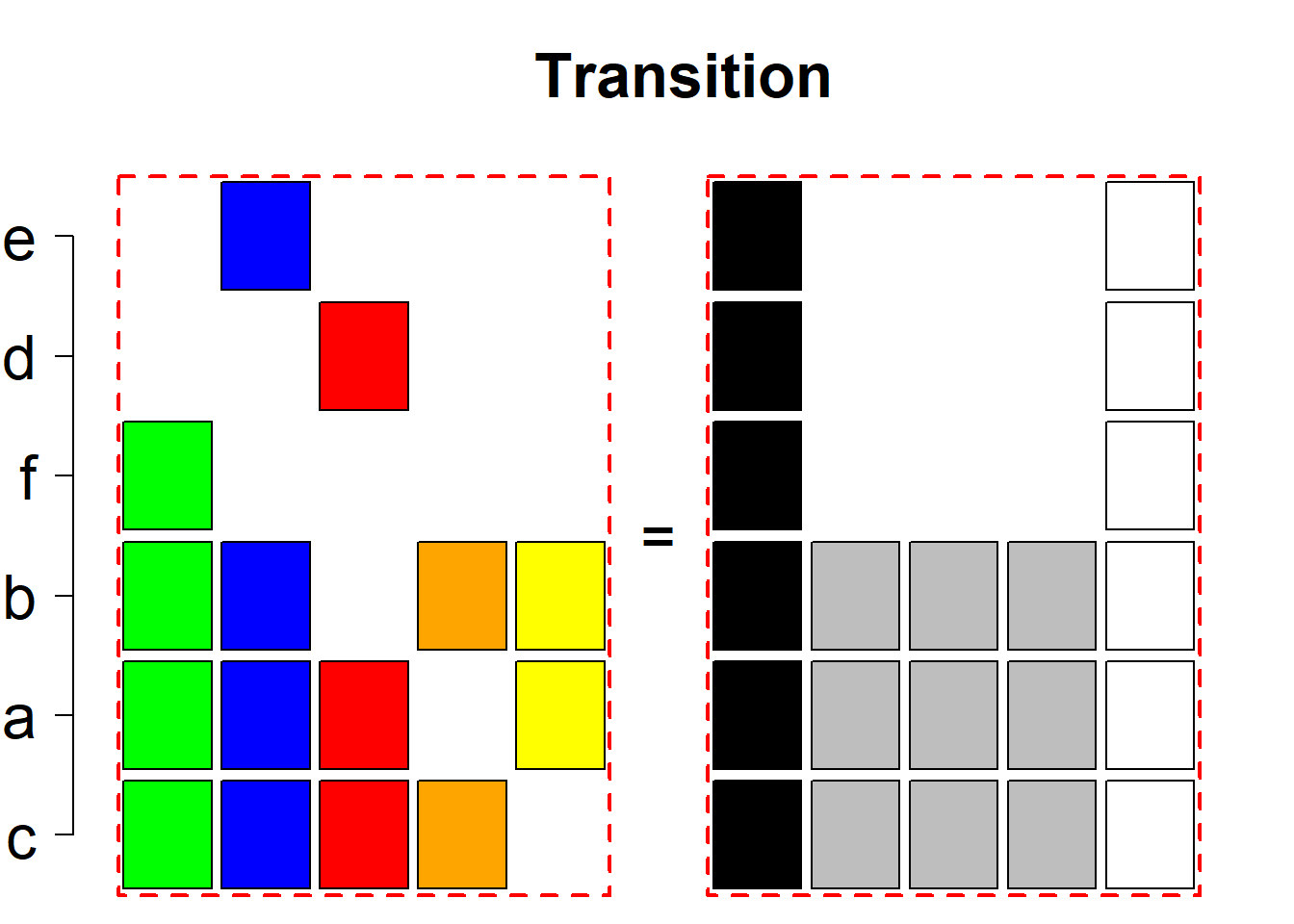
Each permutational type is labeled by a formal arithmetic expression which encodes the cardinalities of involved sets. The number of involved set systems in a permutation type is in the bracket followed. Two mutually complementary permutational types are on the same hyper-row, represented by the left and right diagrams in the hyper-row. The middle diagram in the hyper-row is auxiliary, to describe the transition from the type on the left-hand side to its complementary type on the right-hand side. Specifically, the middle diagram describes just the complementary system to the system in the left diagram, and labels of its rows encode the permutation of variables (= rows) which leads to the set system in the right diagram.
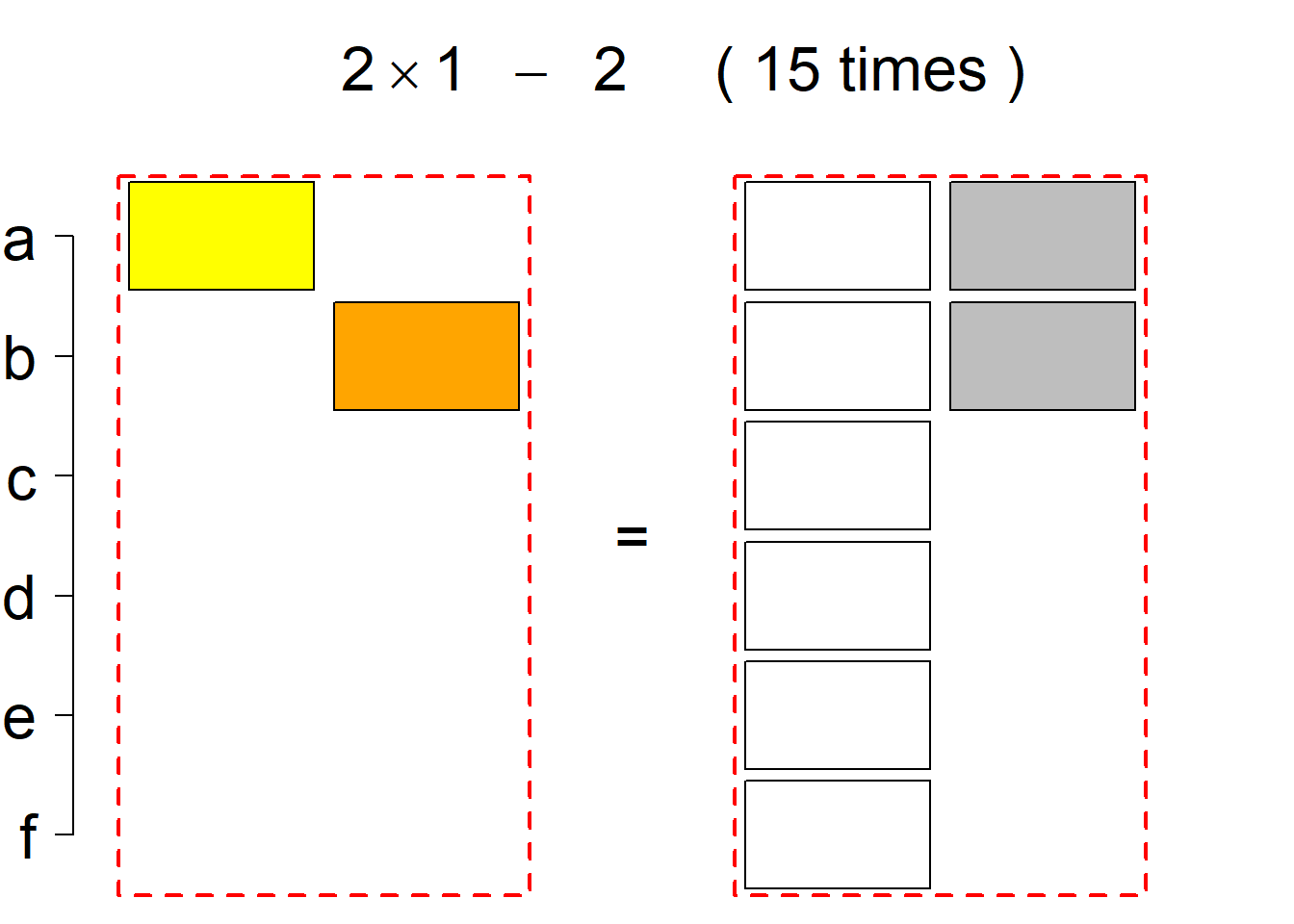
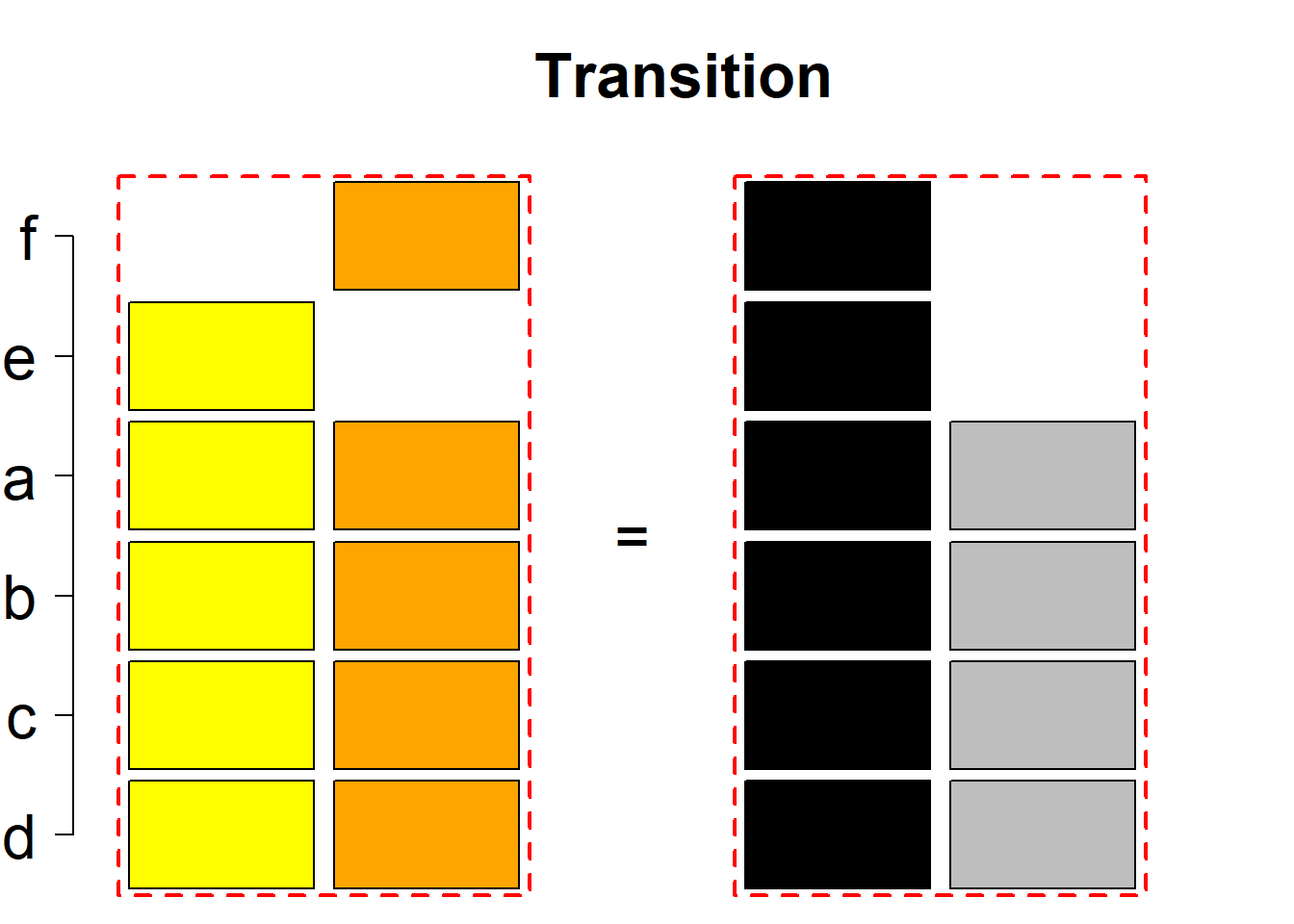
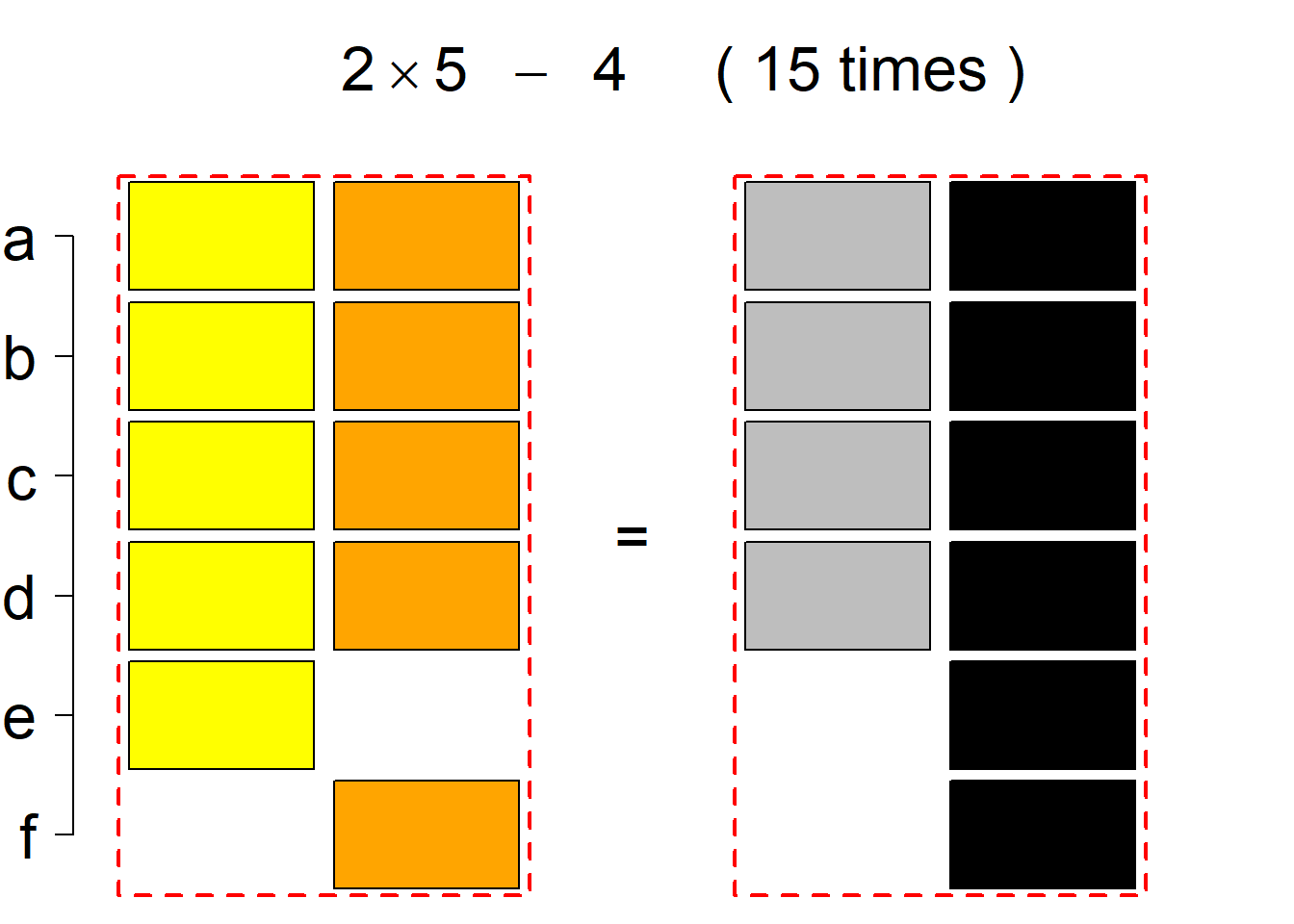
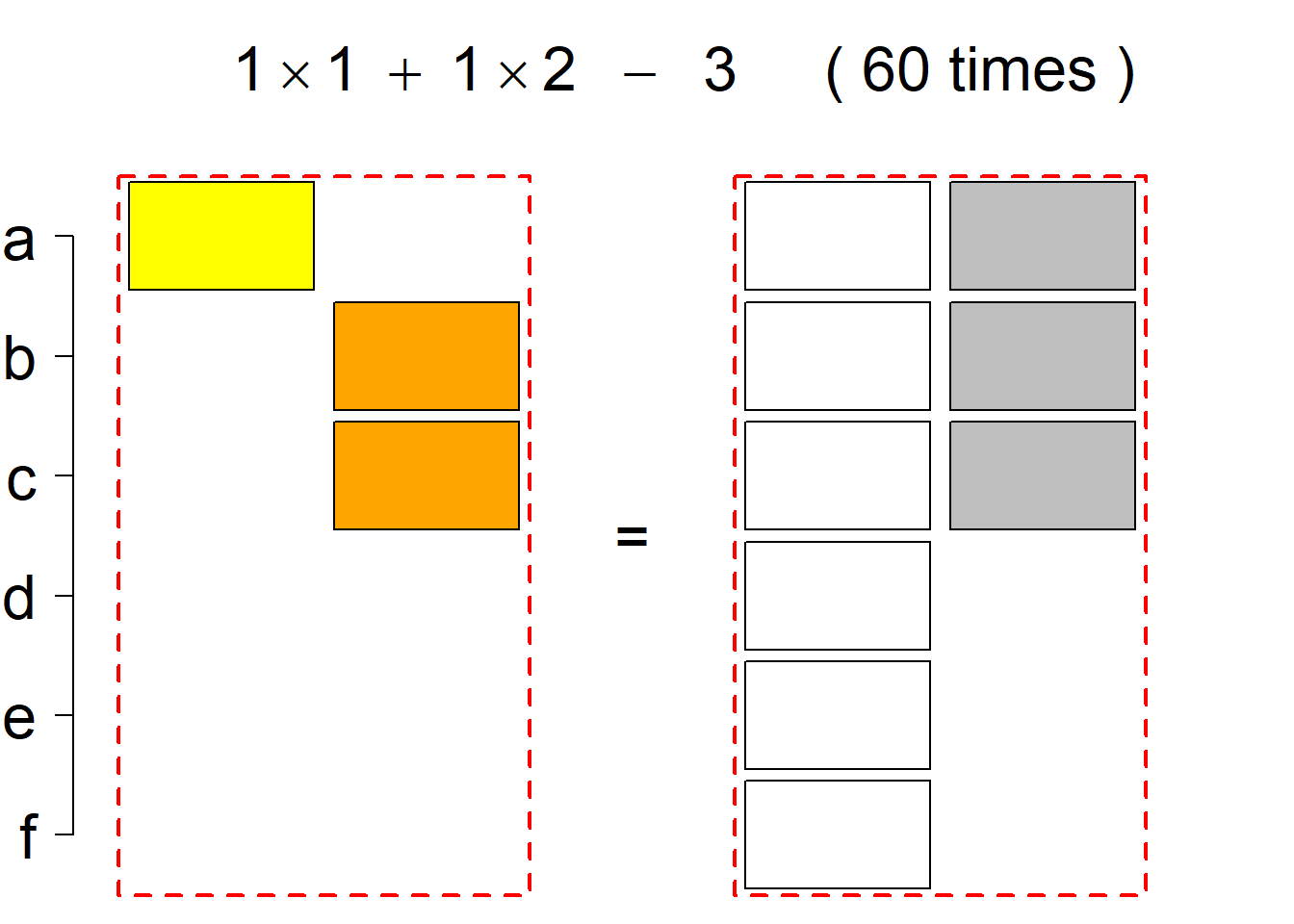
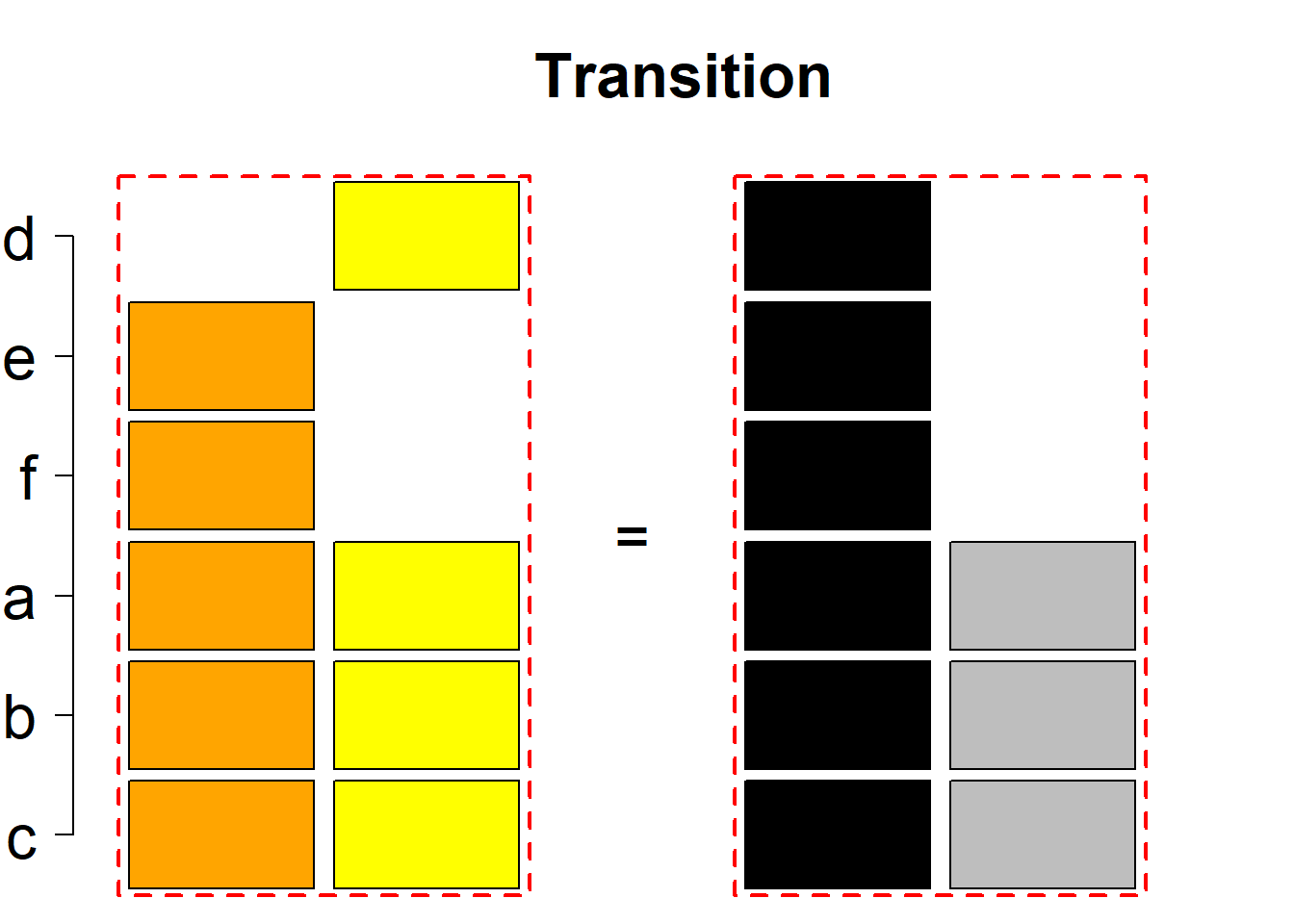
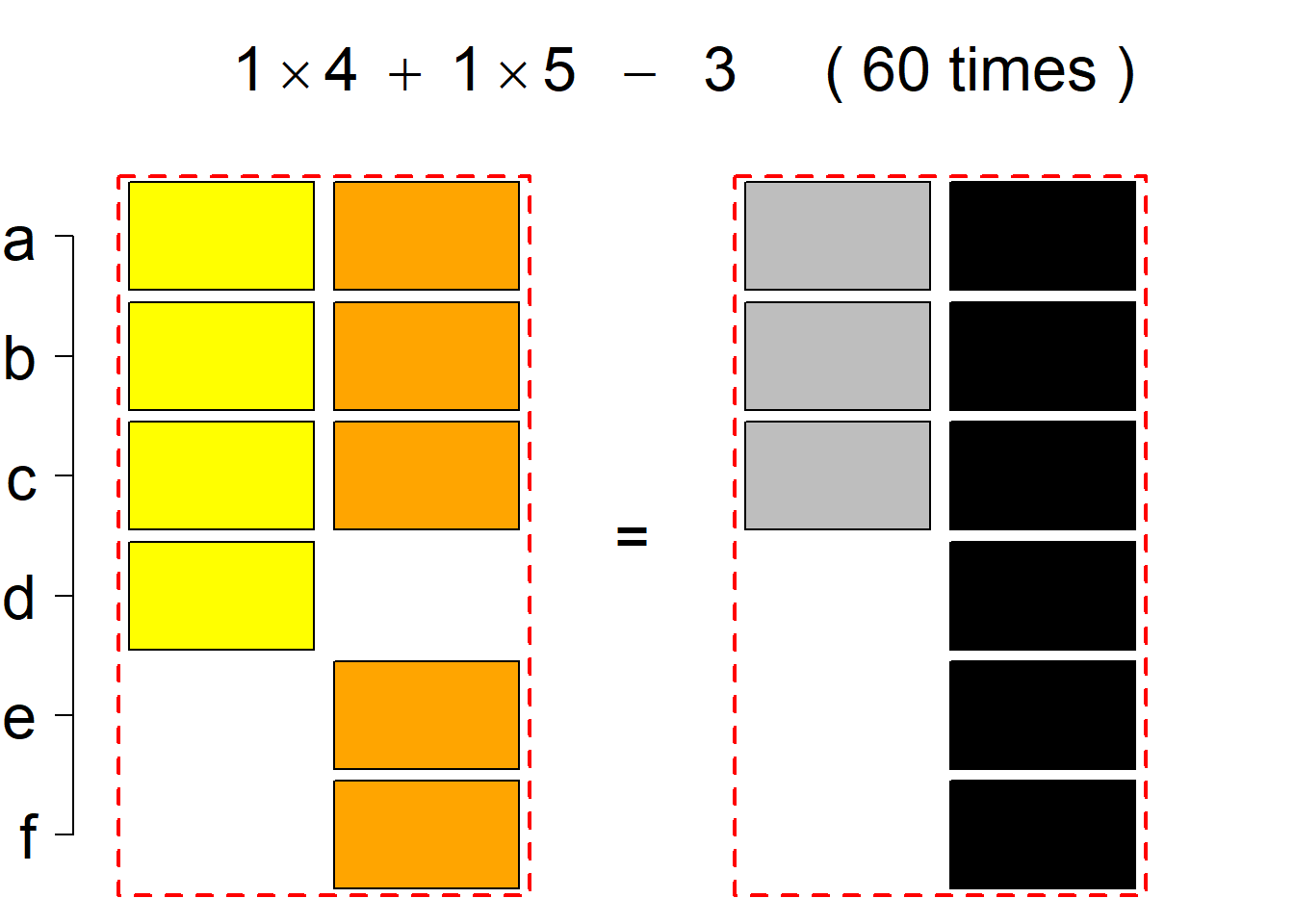
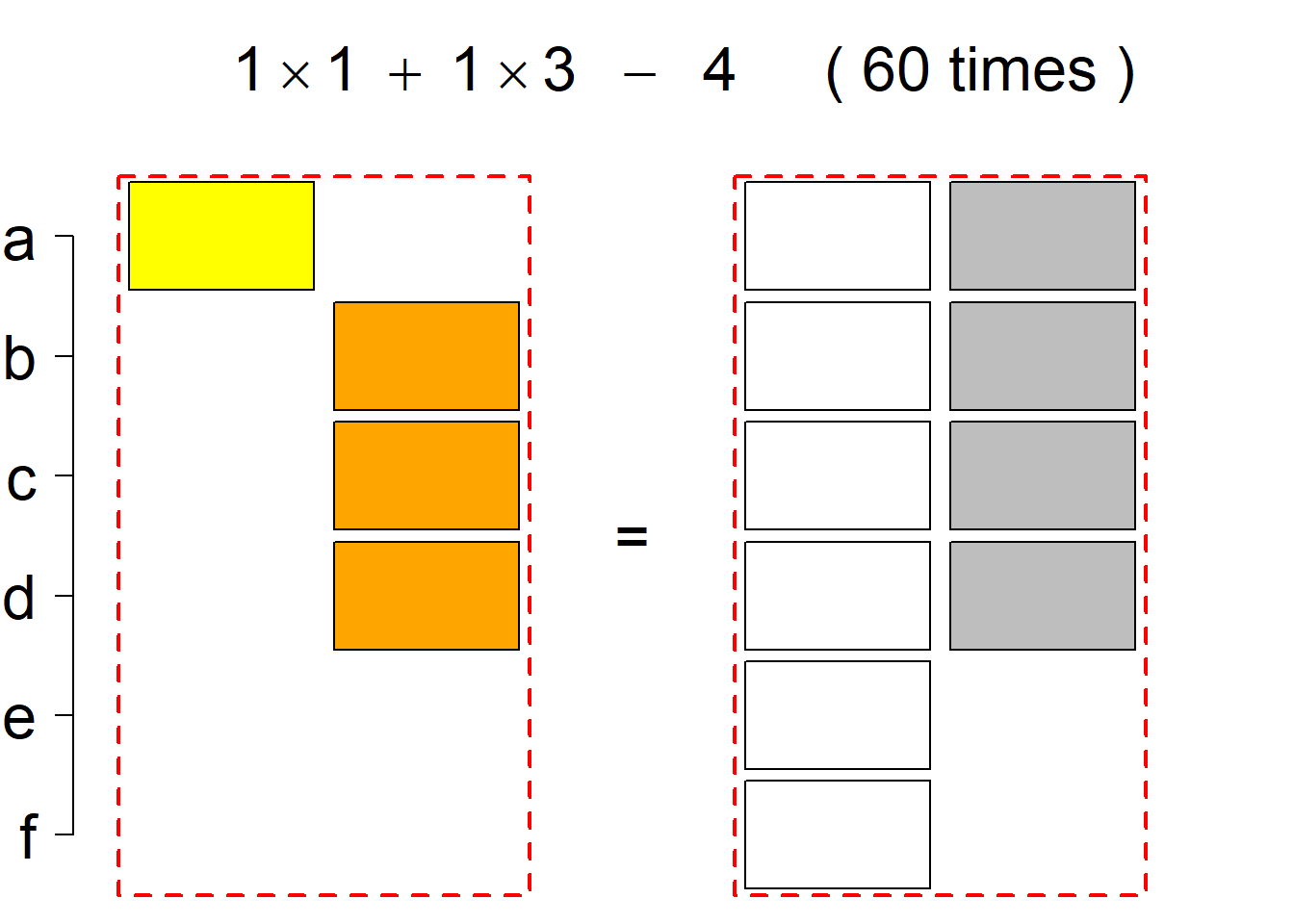

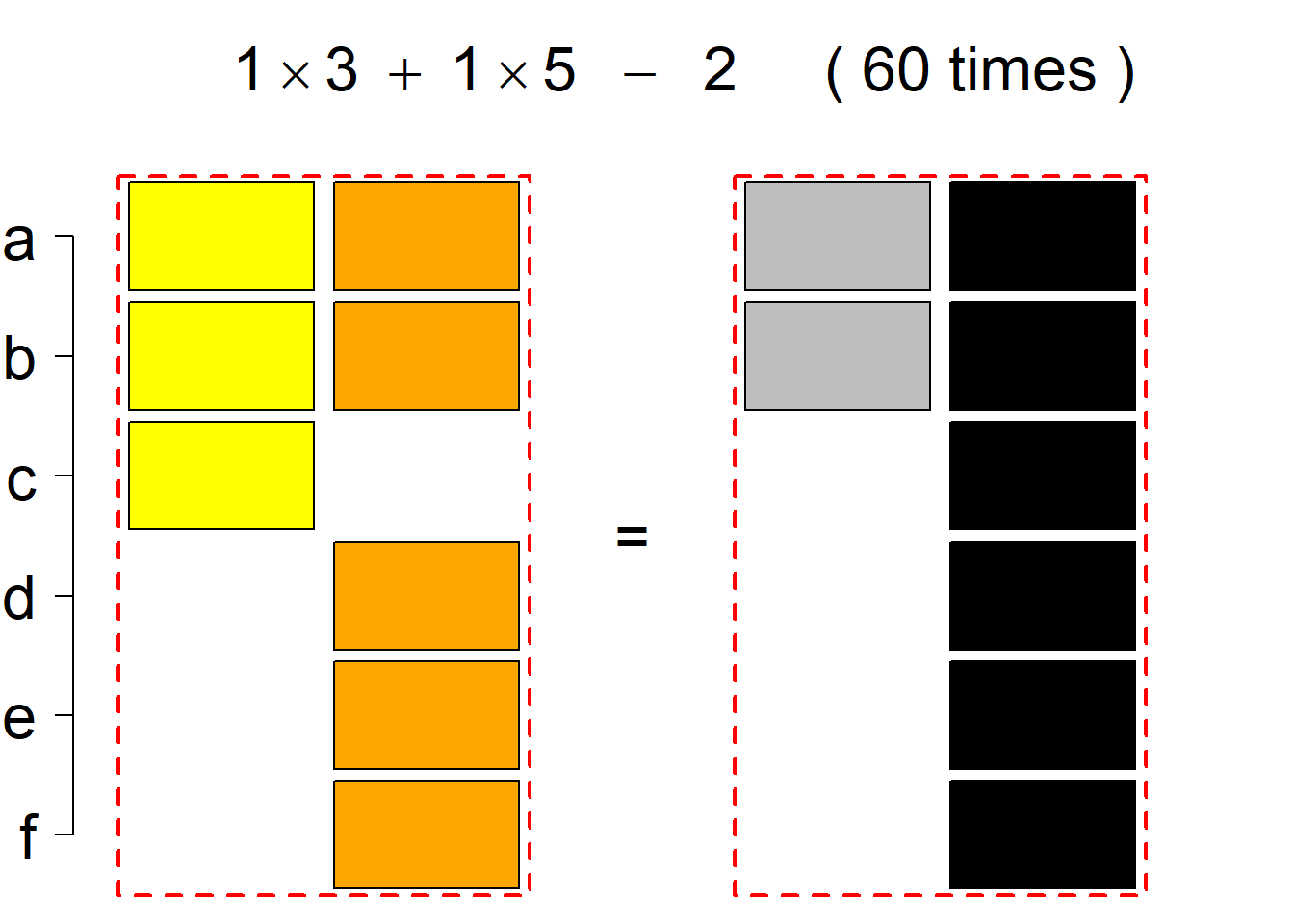
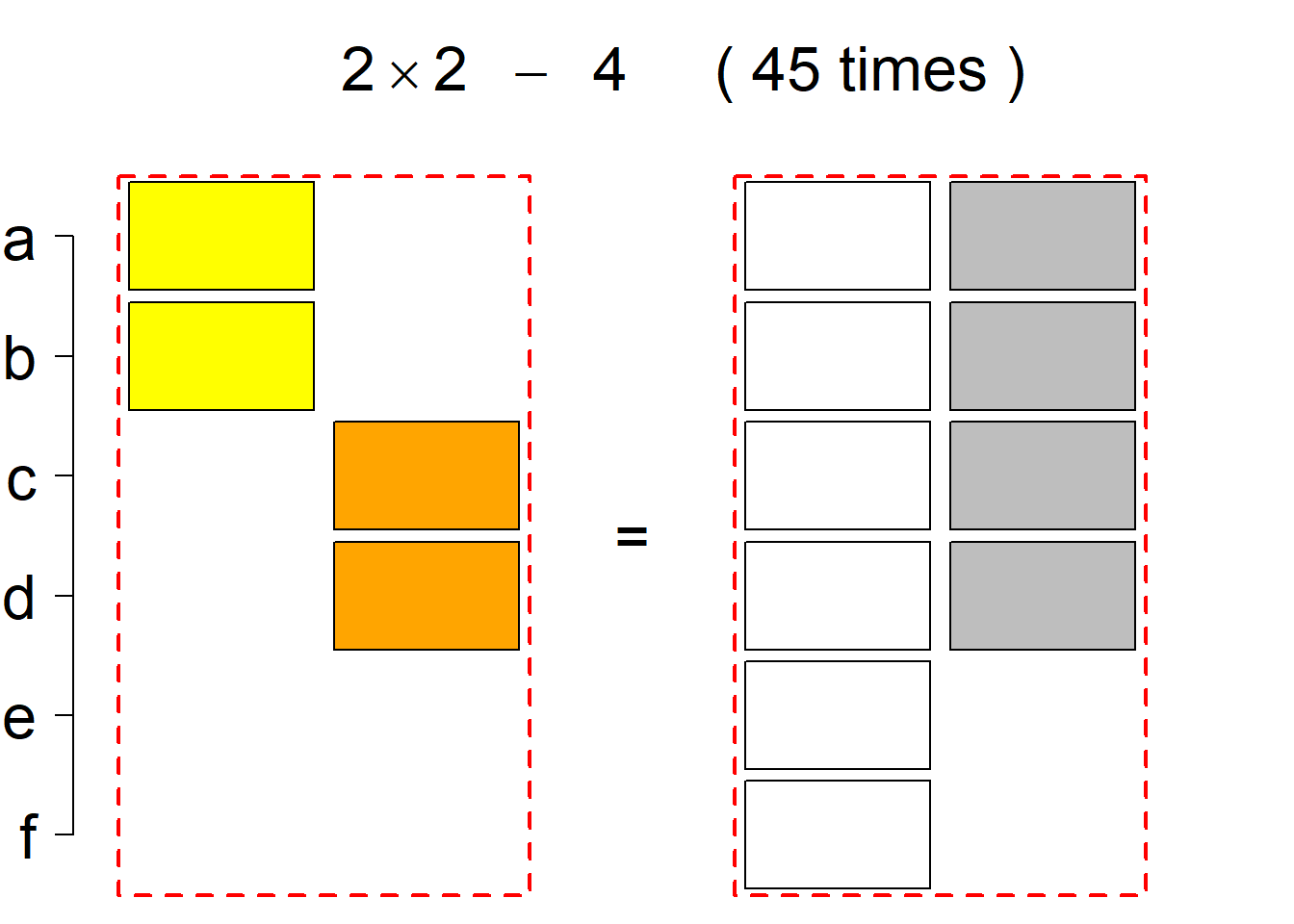
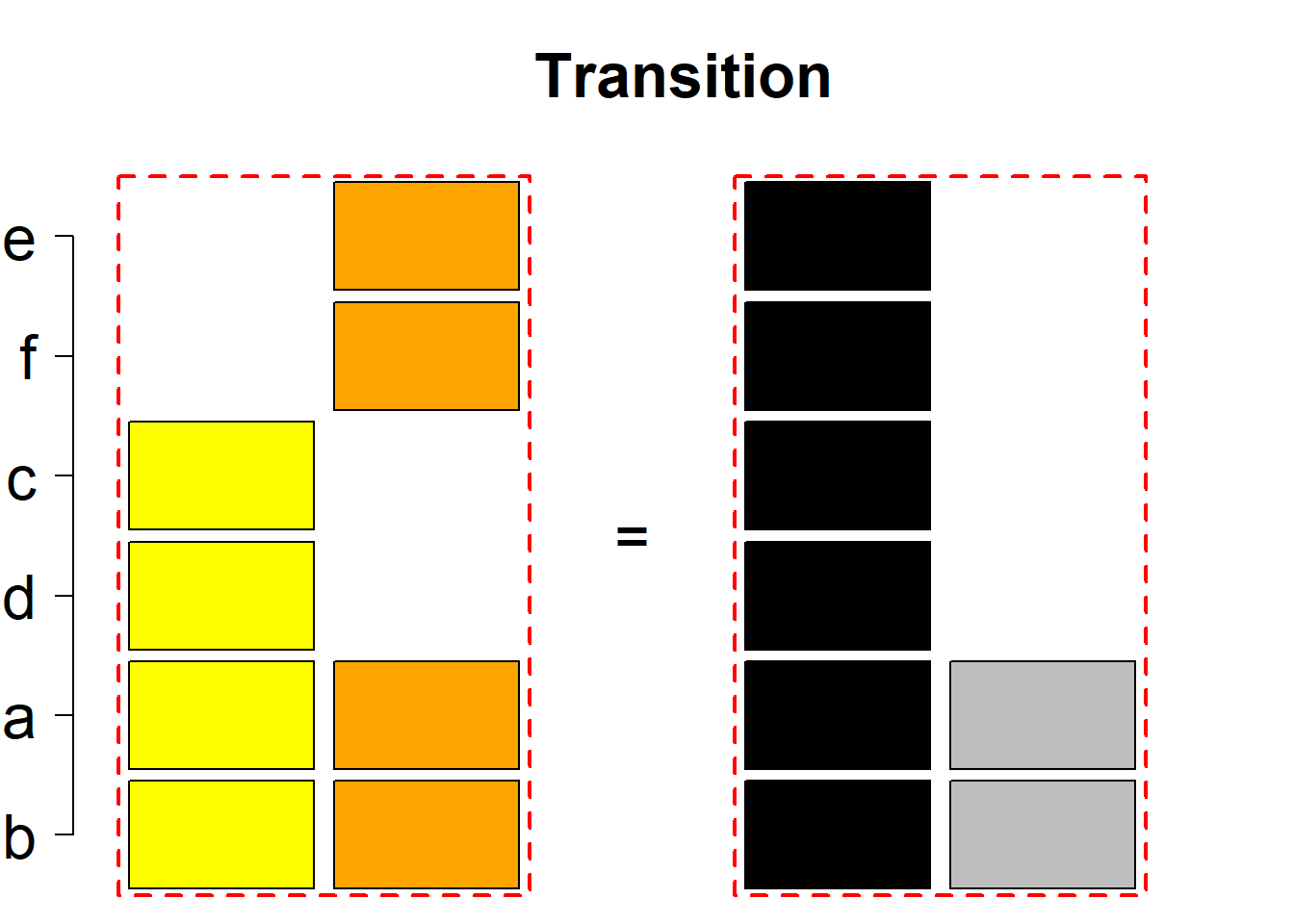
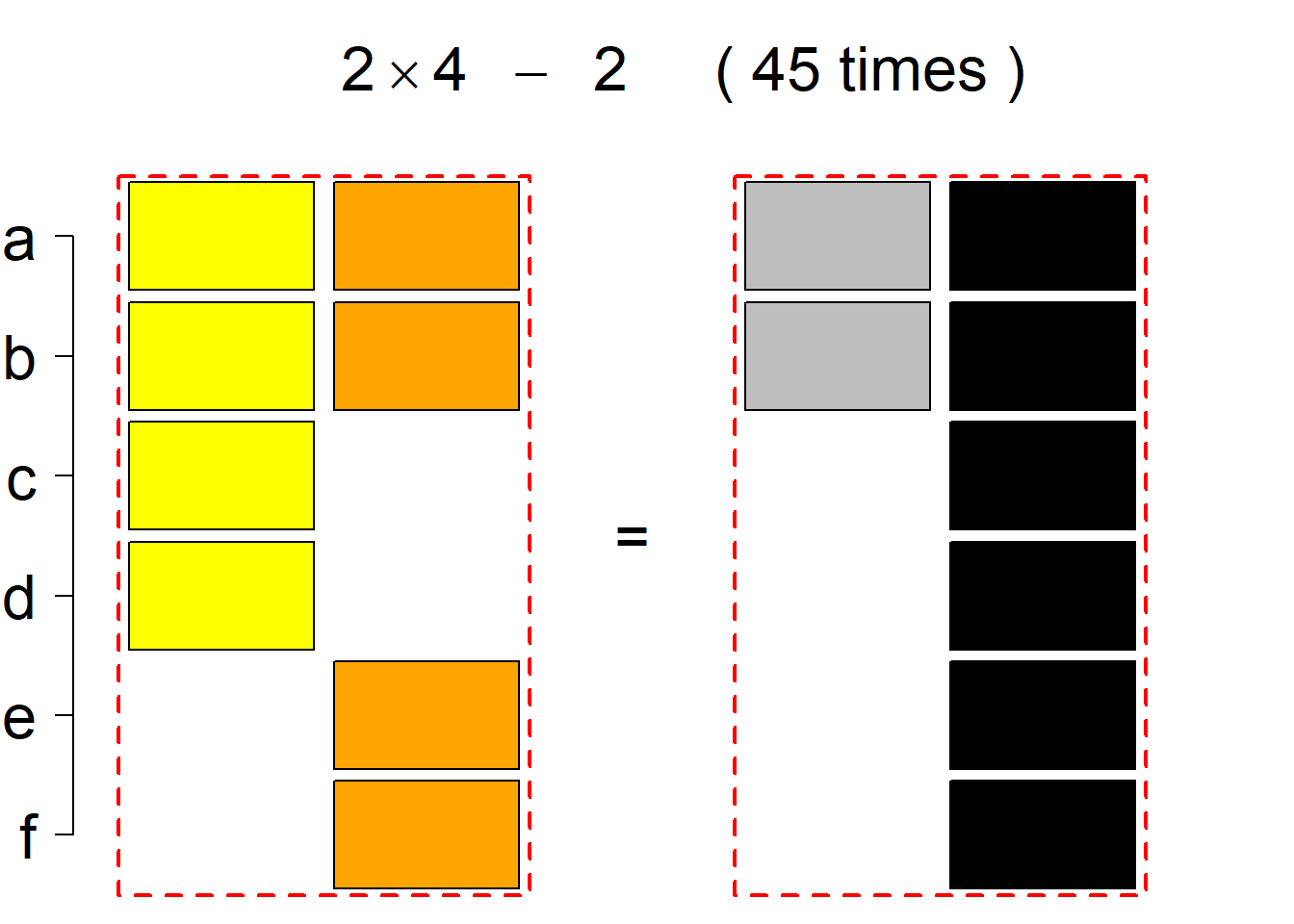
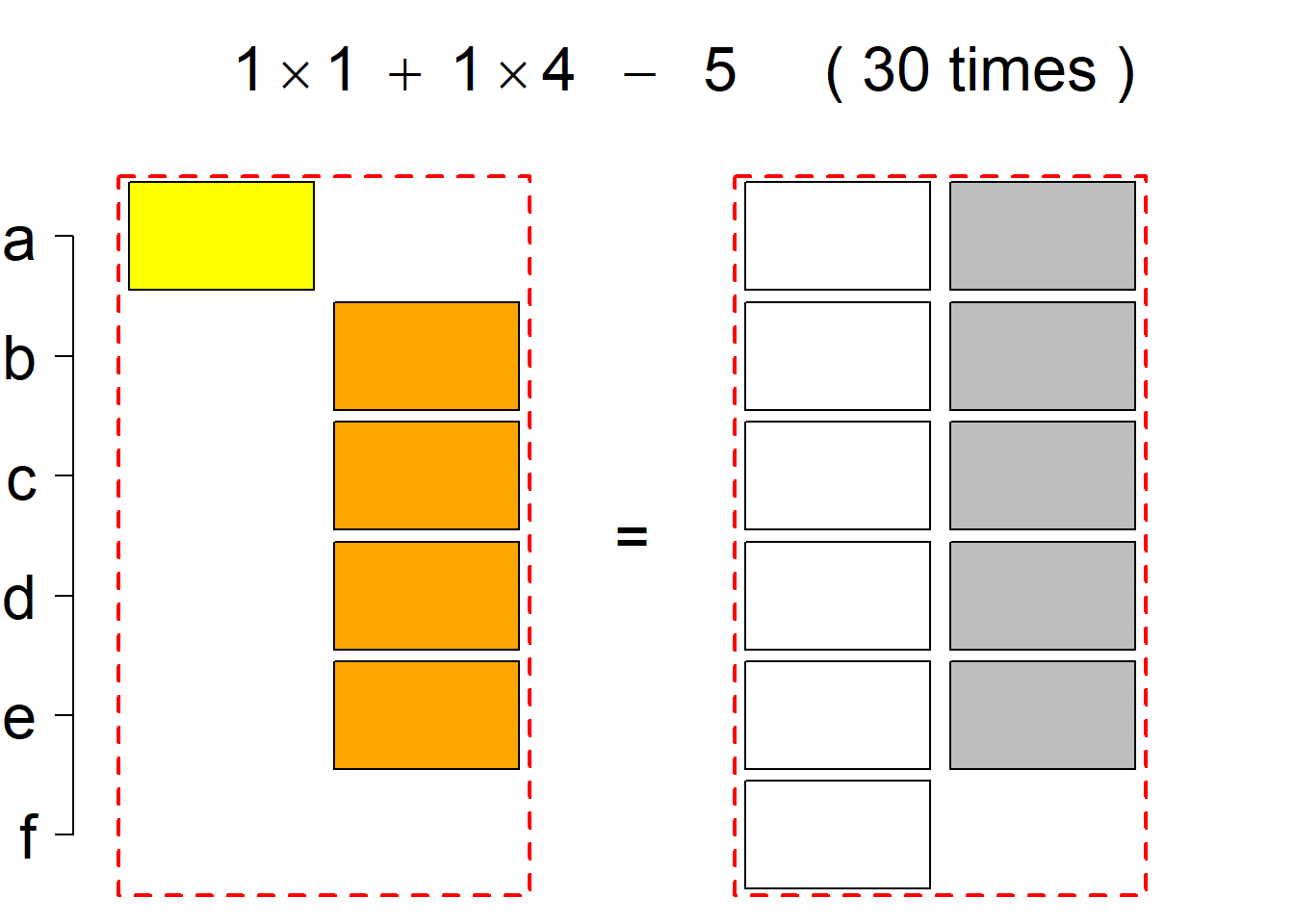

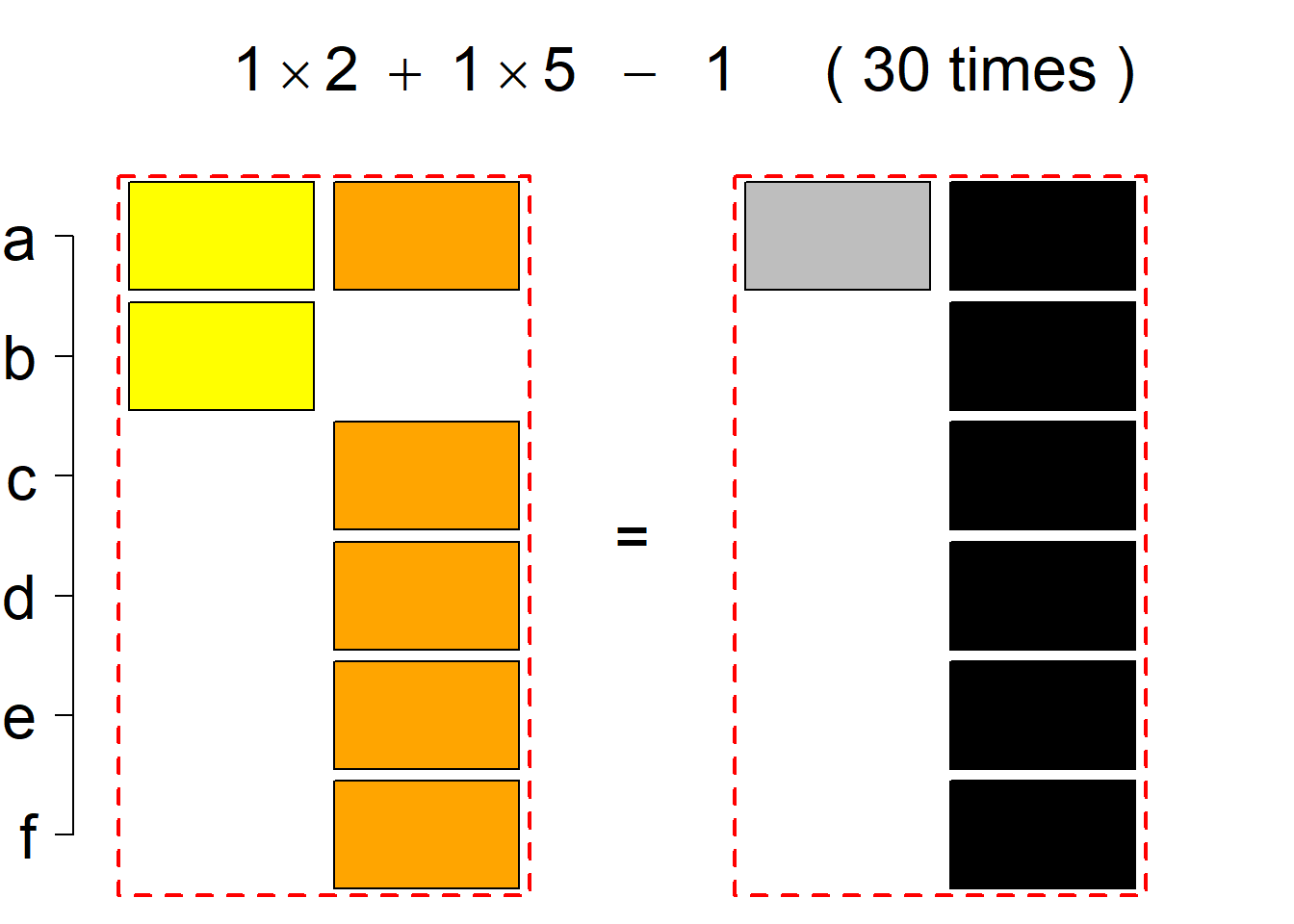
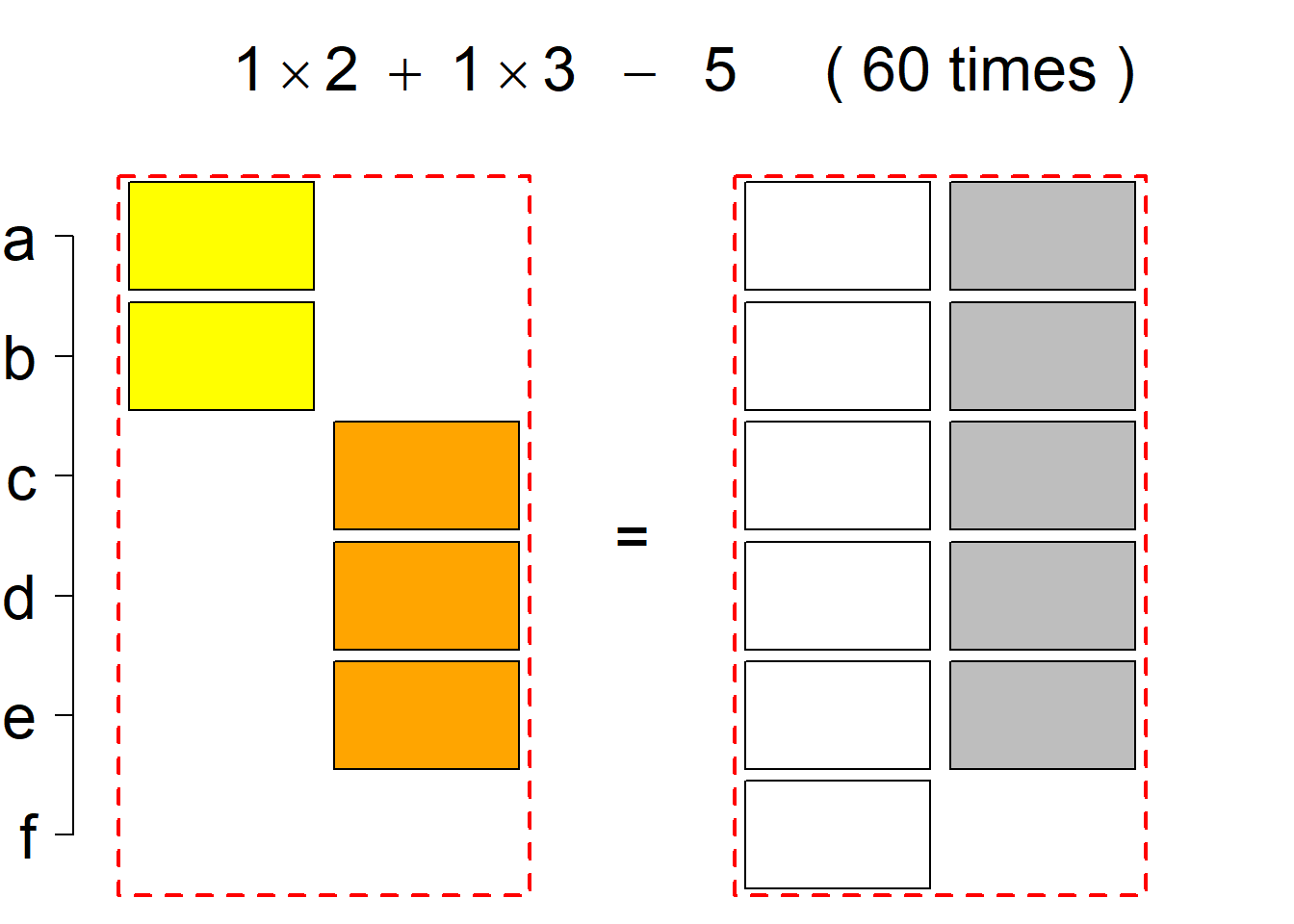
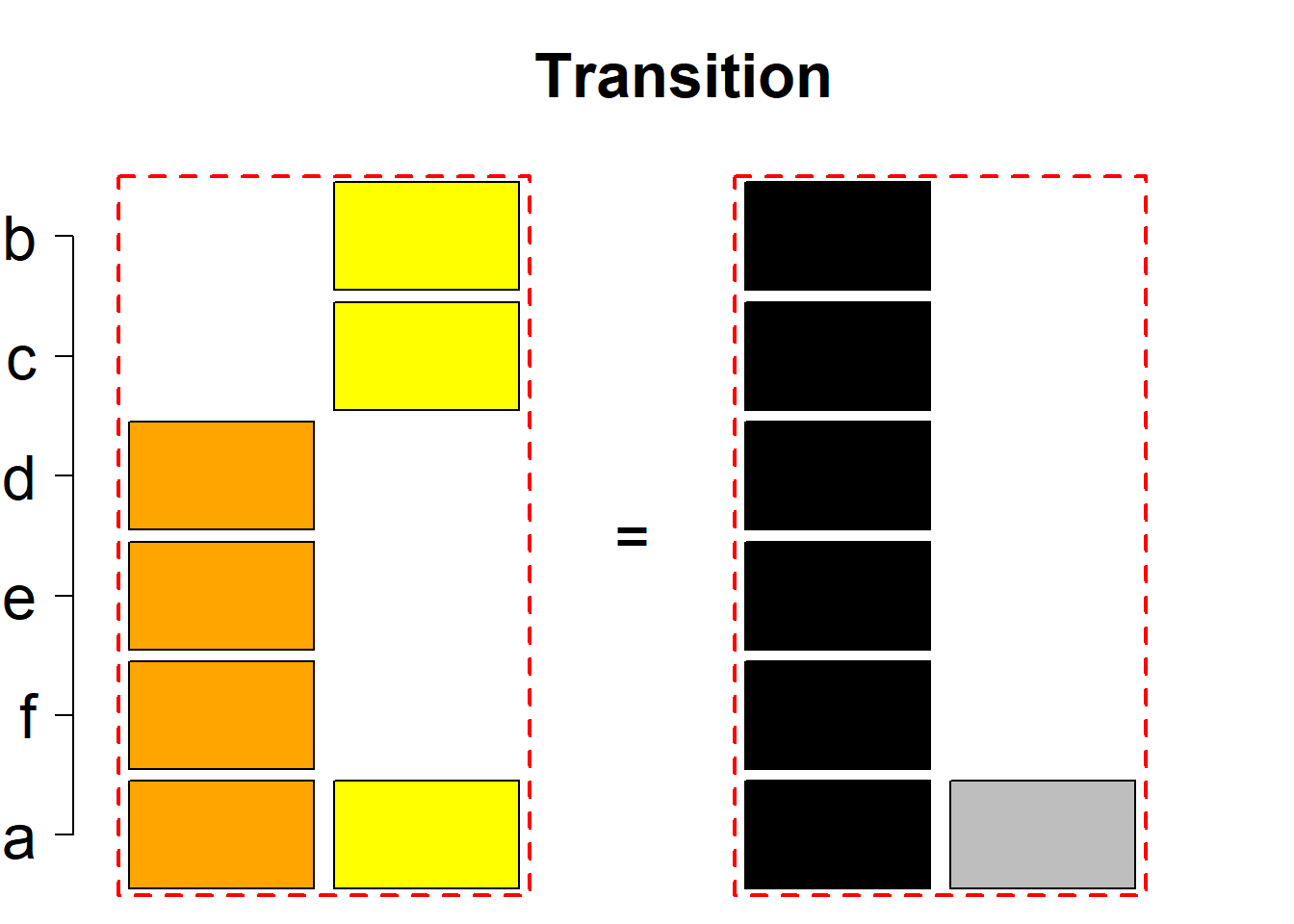


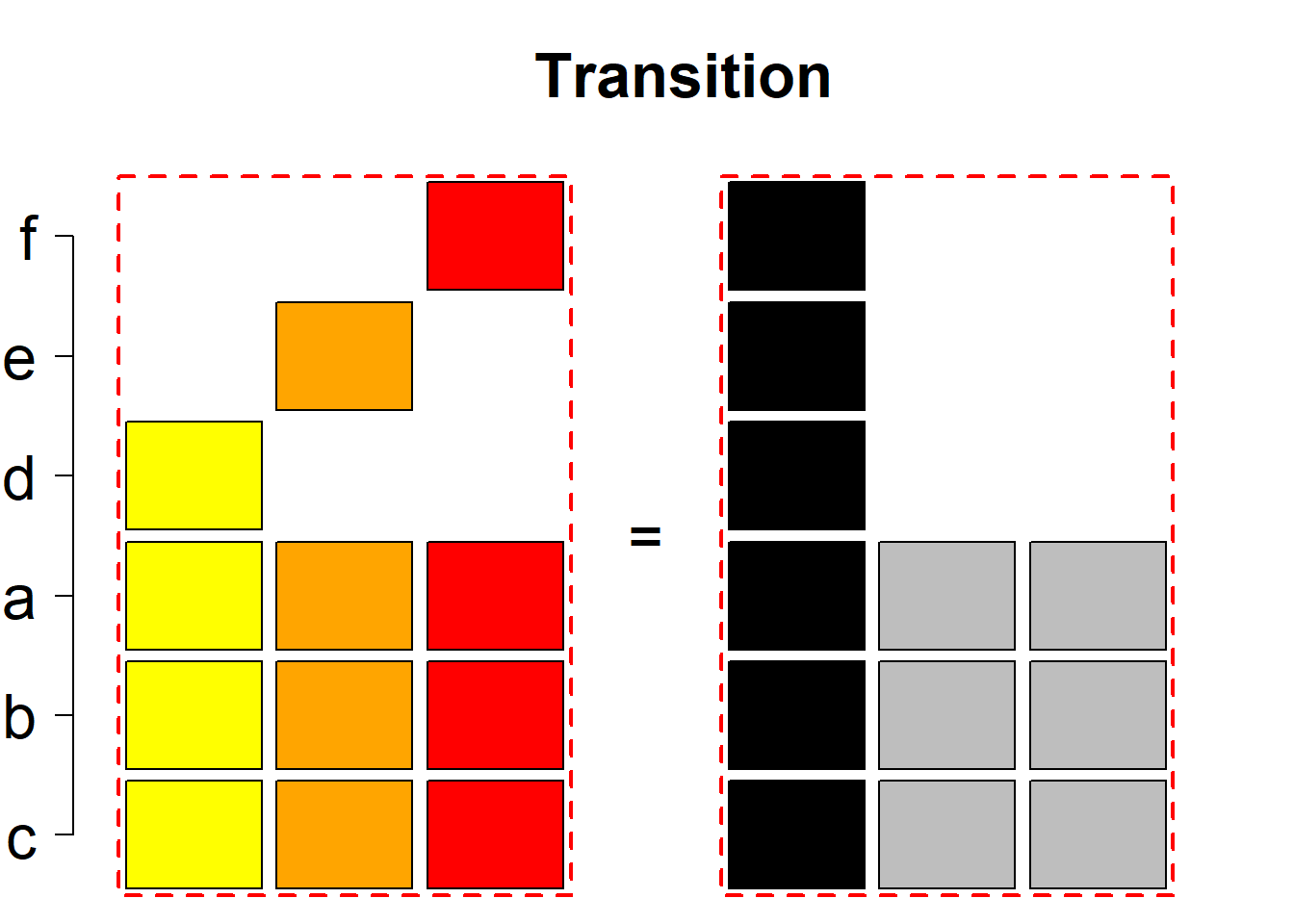
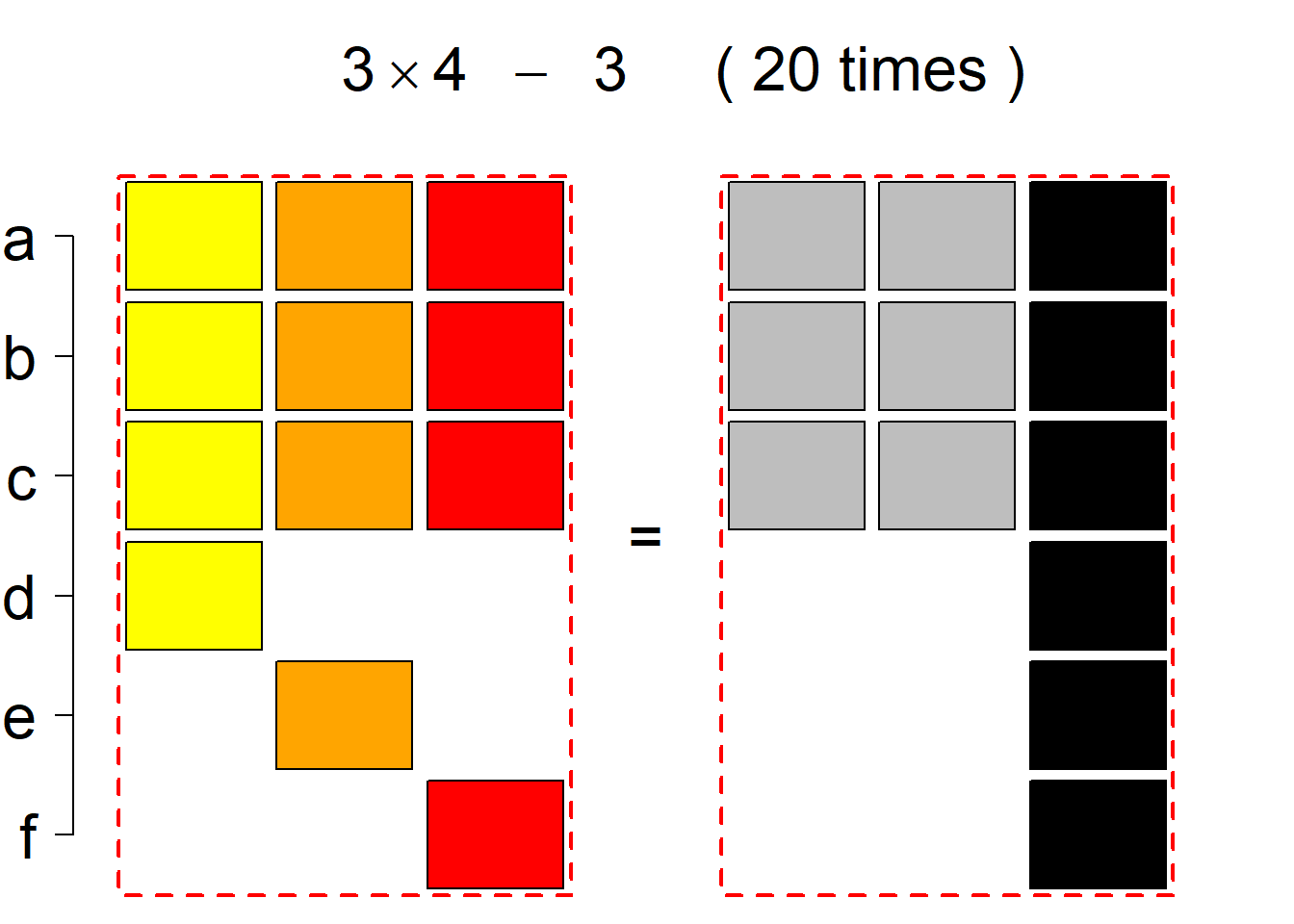

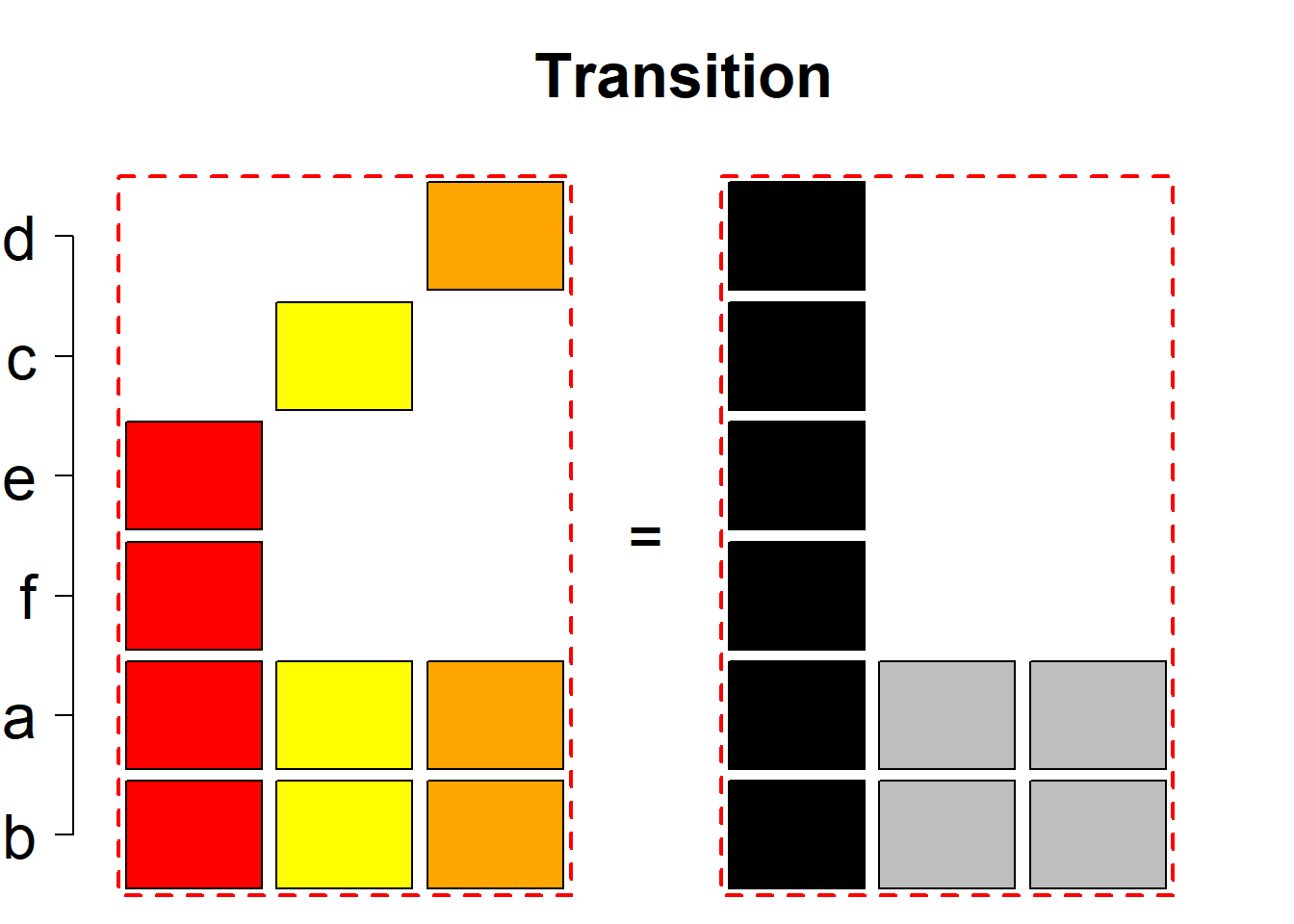
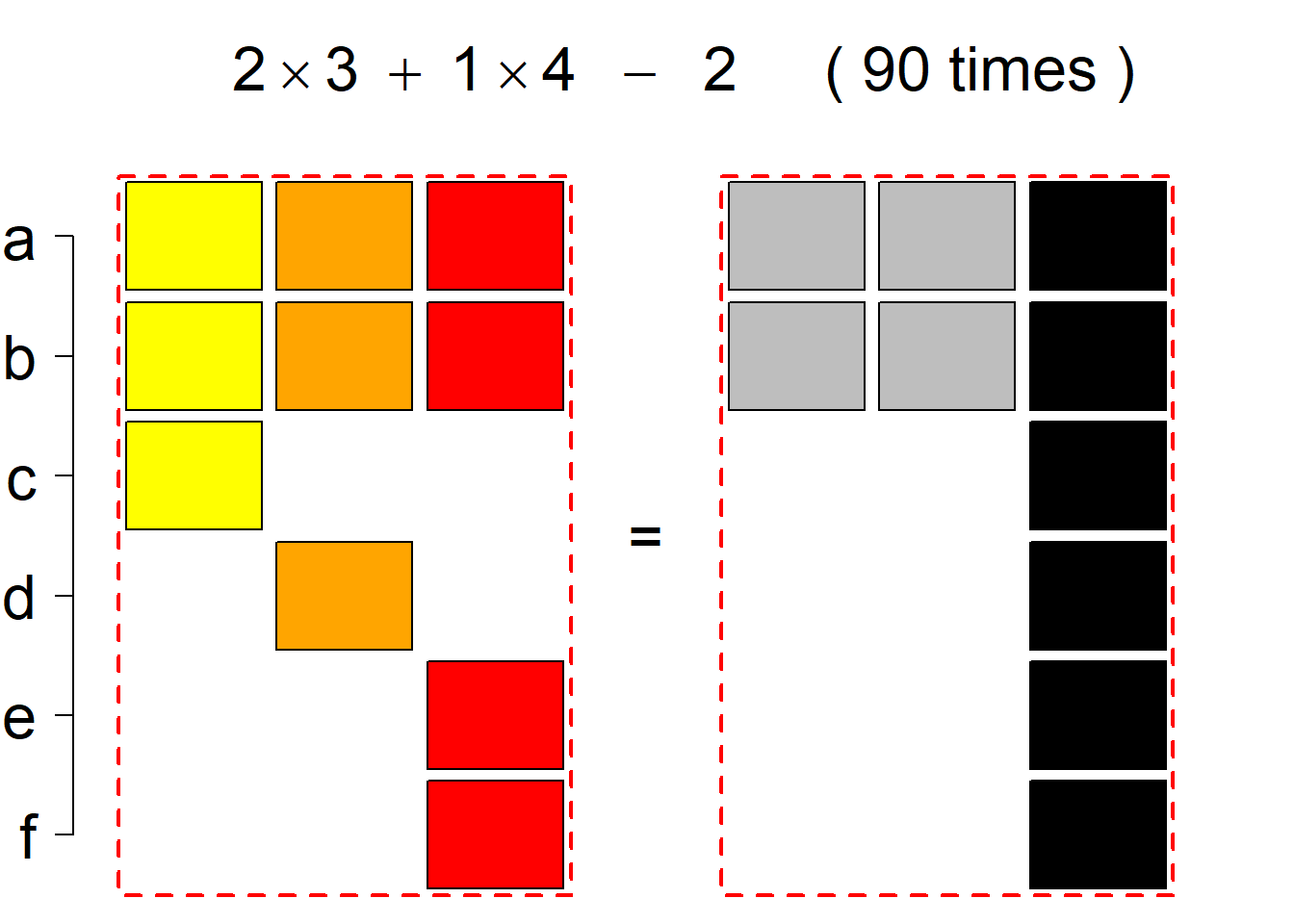
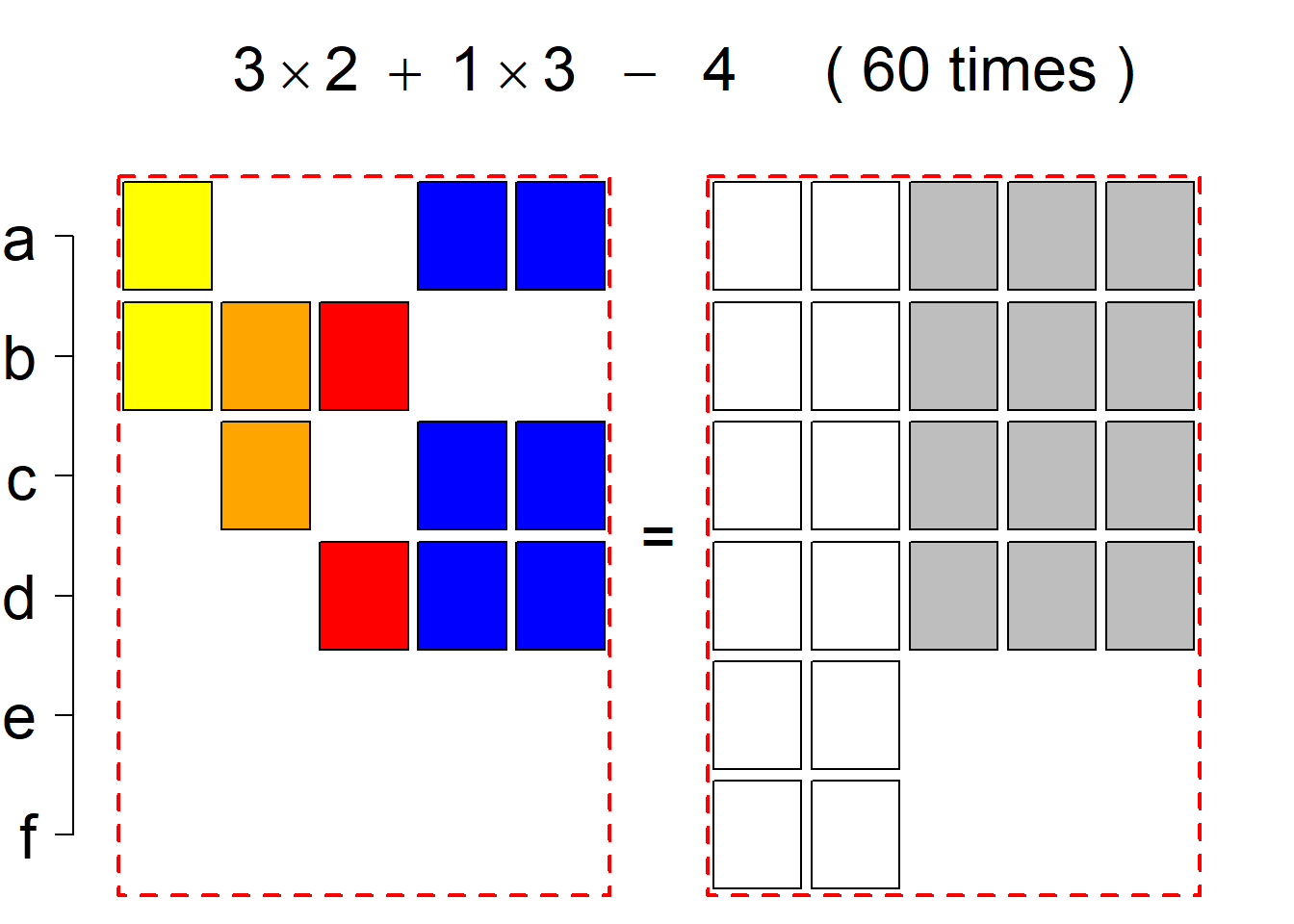
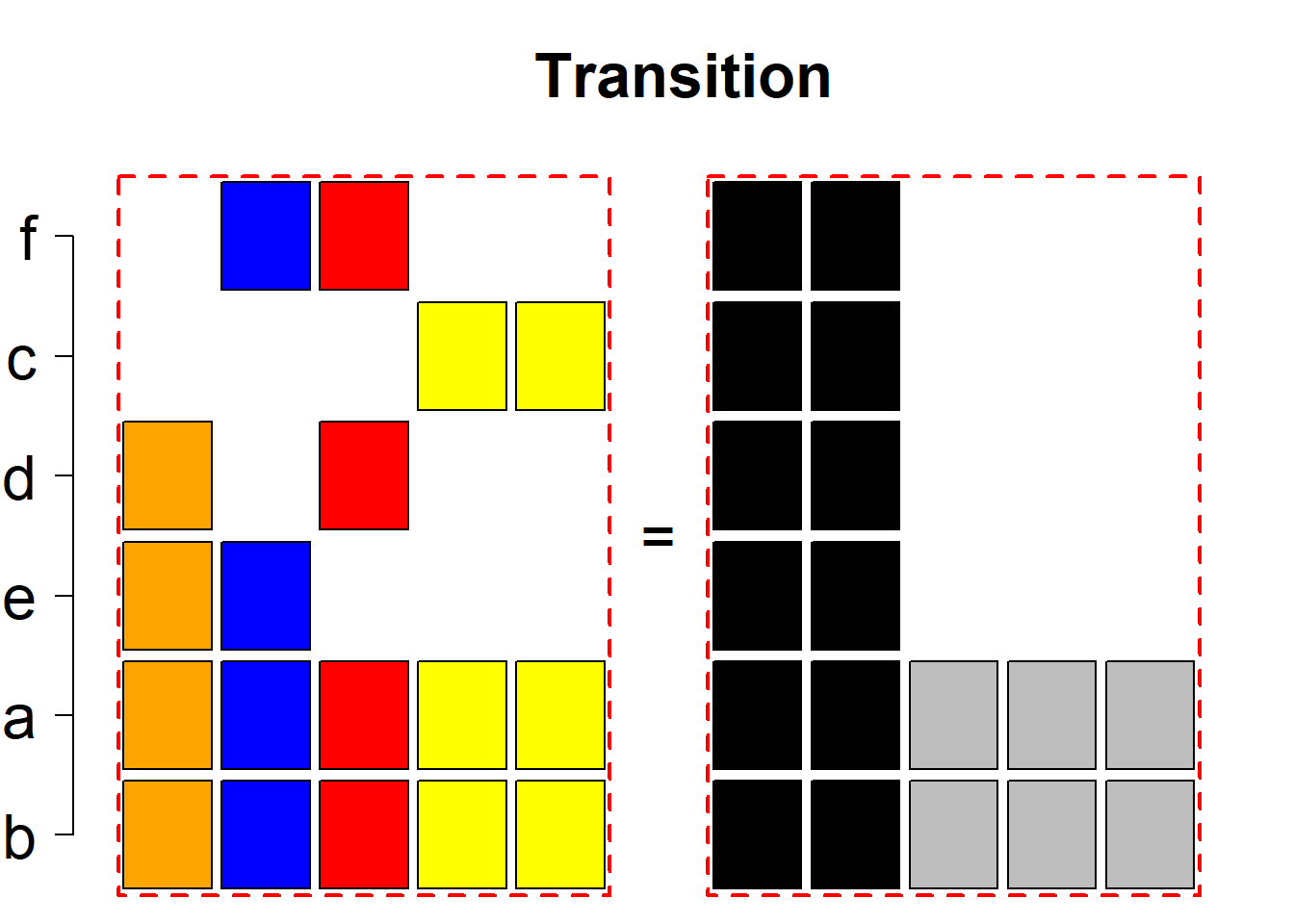
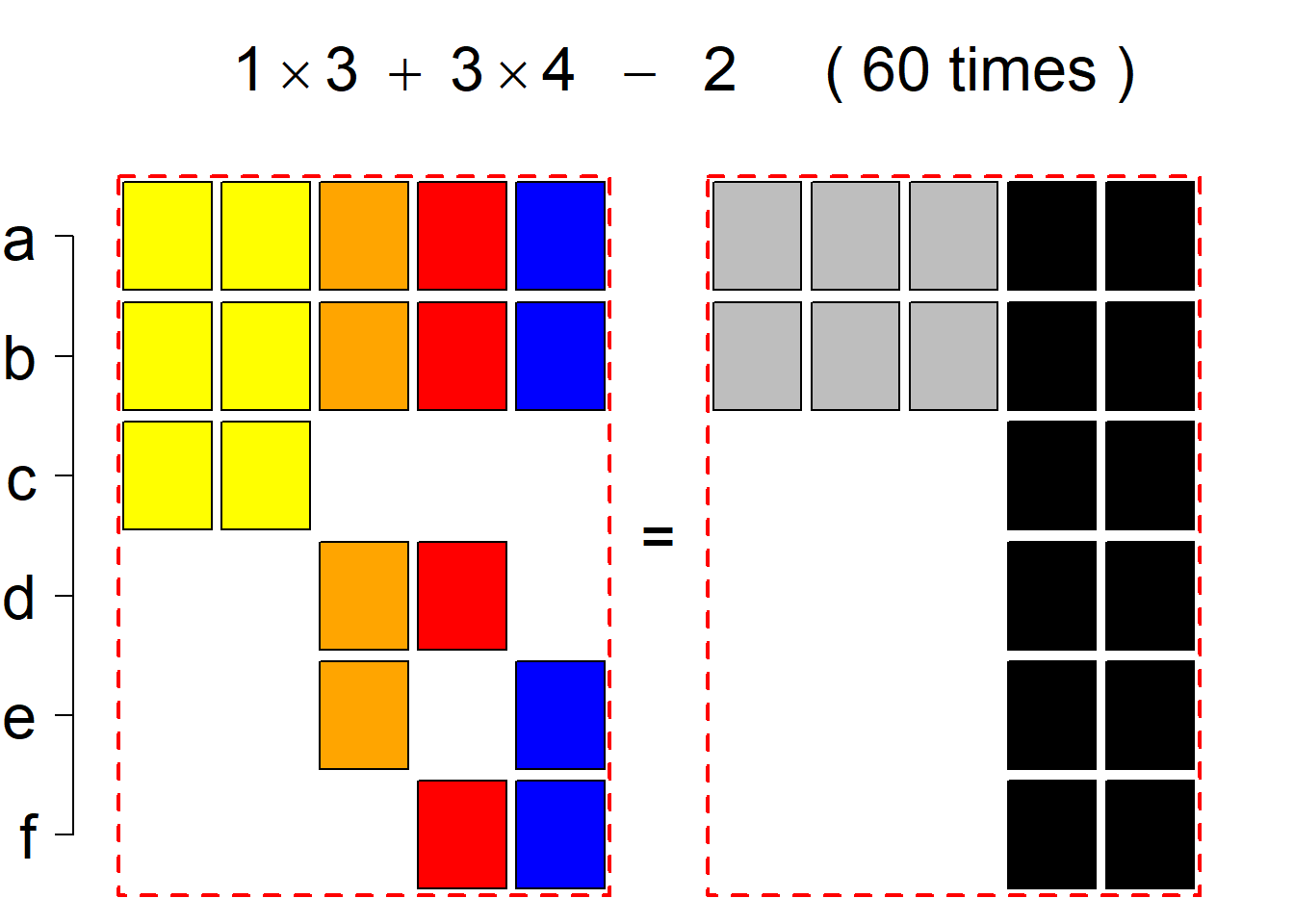
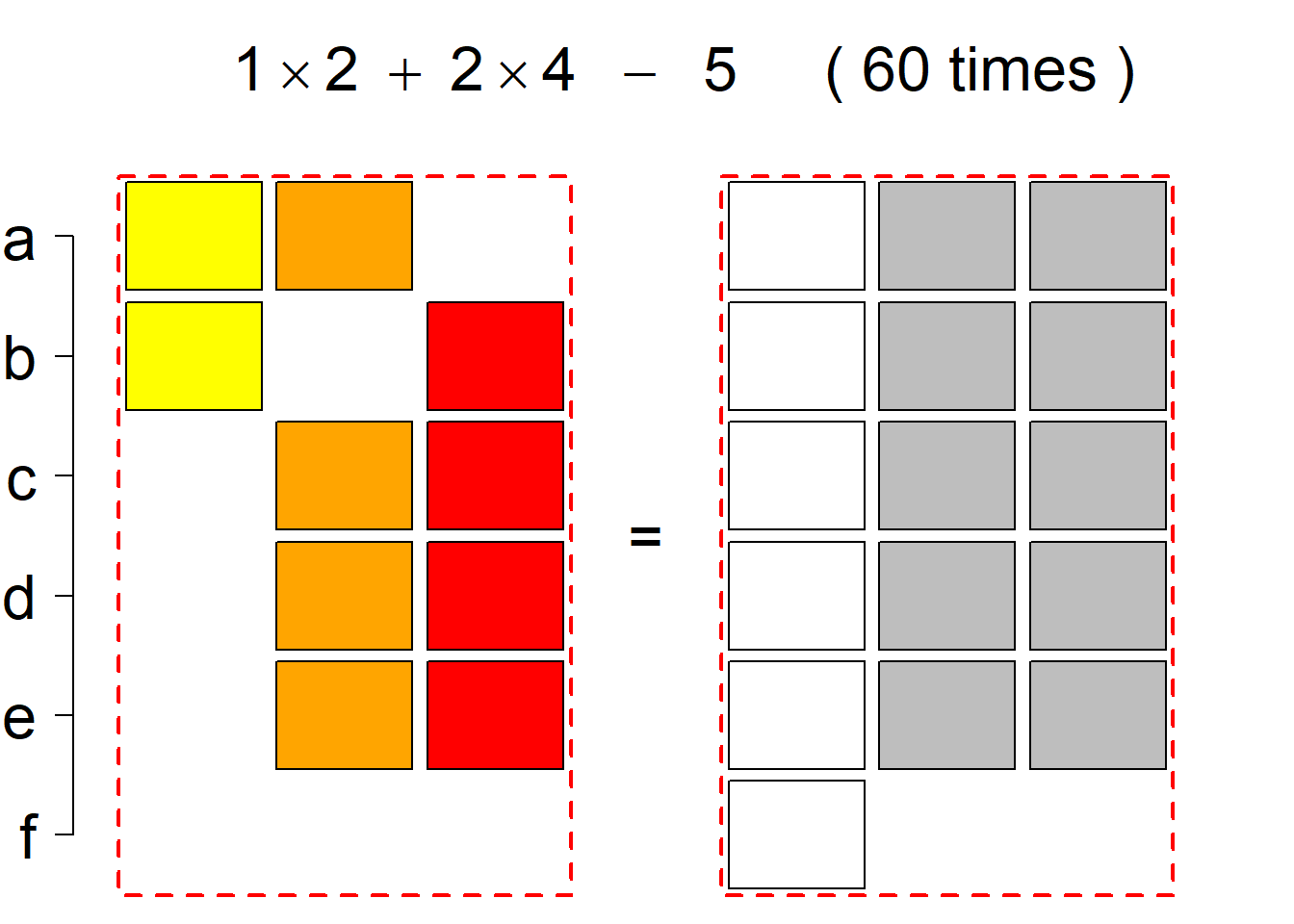


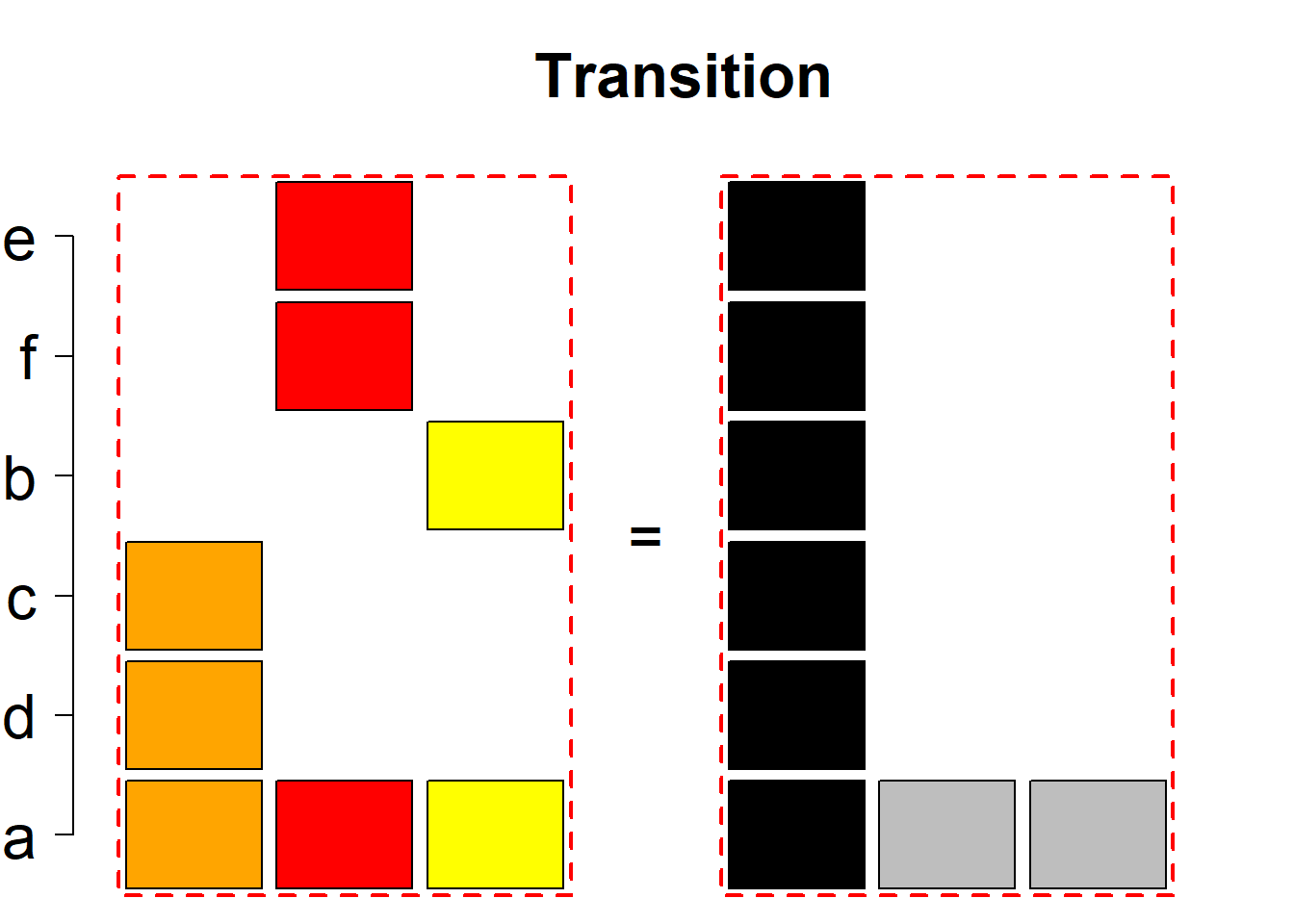
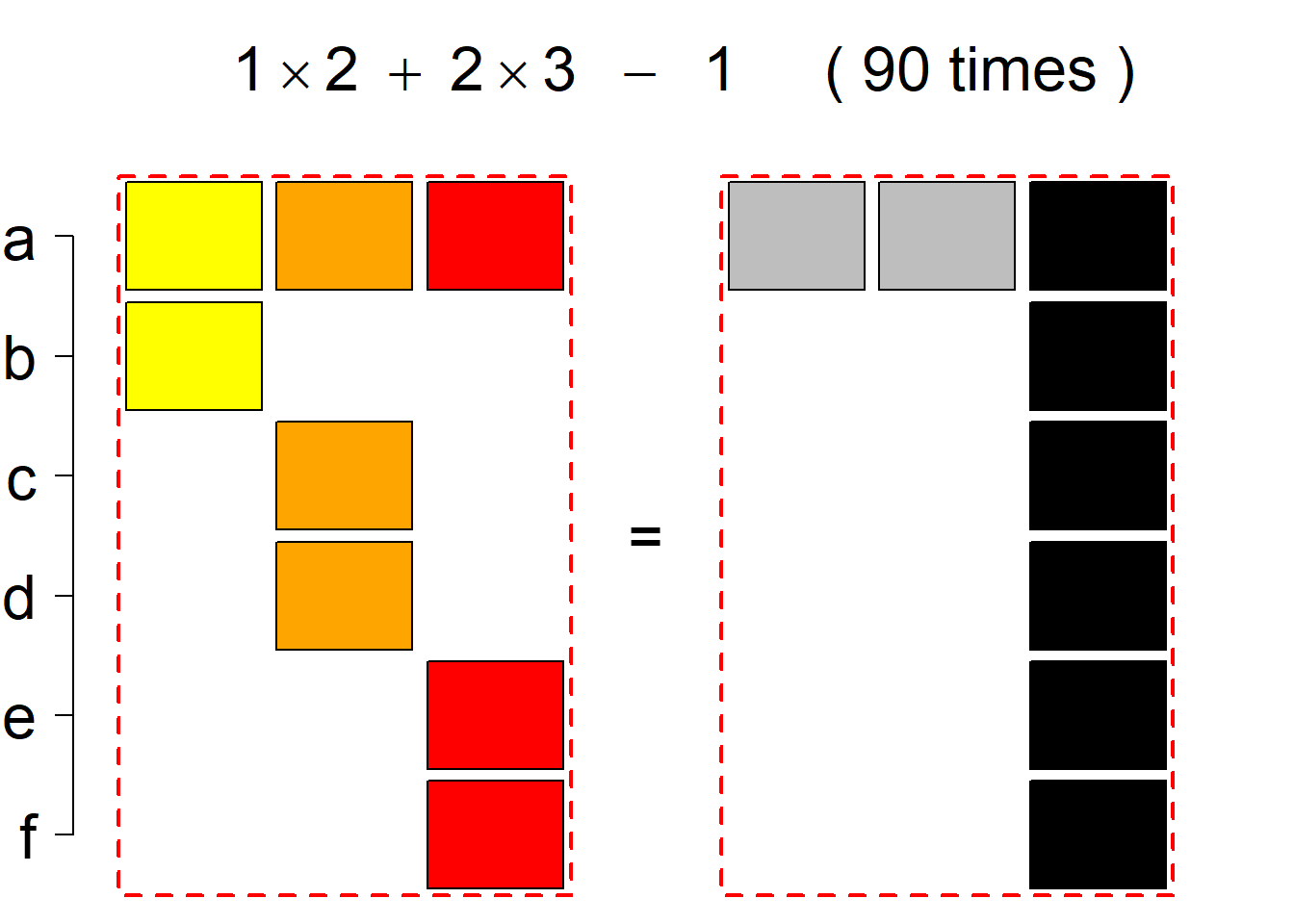


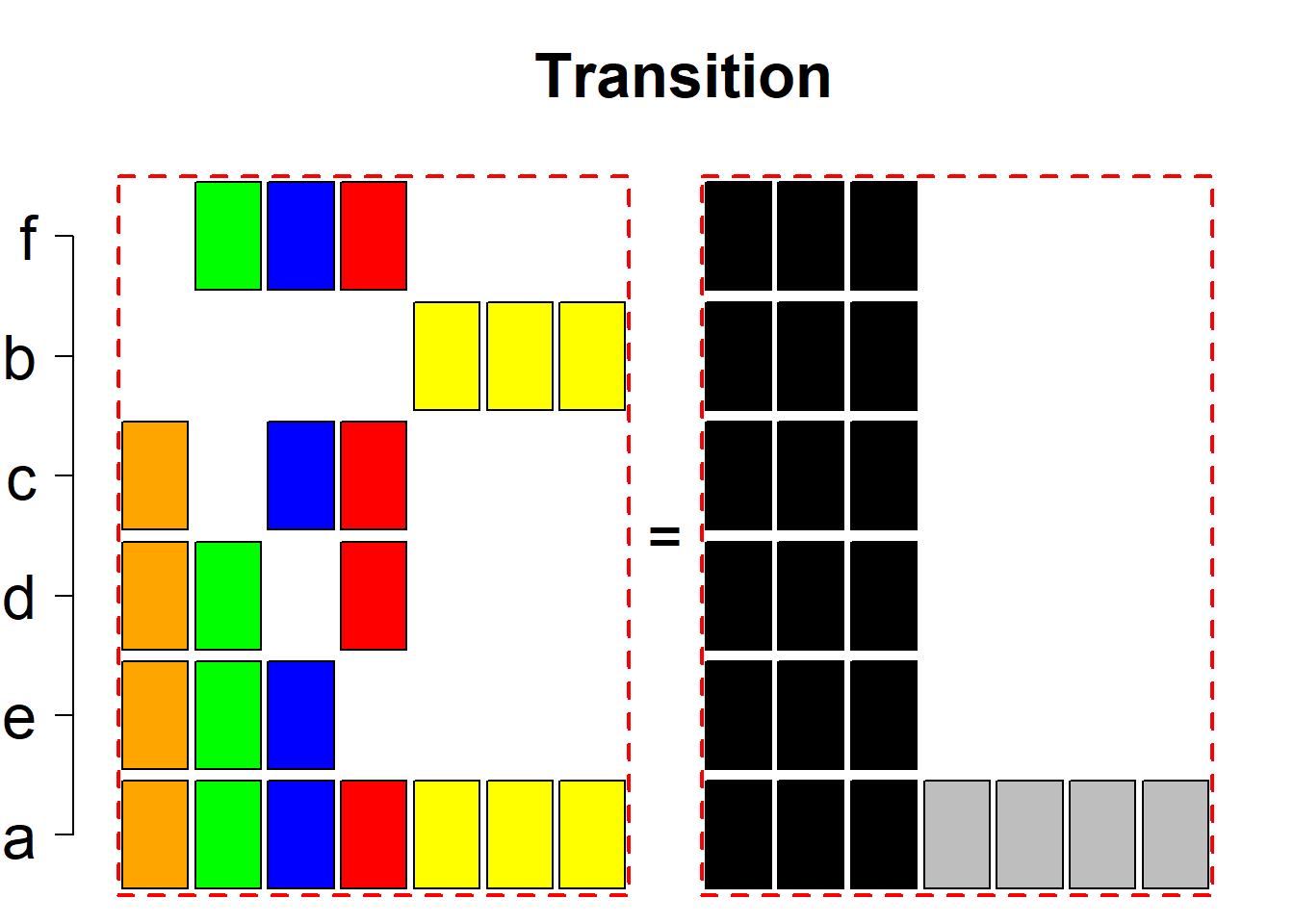
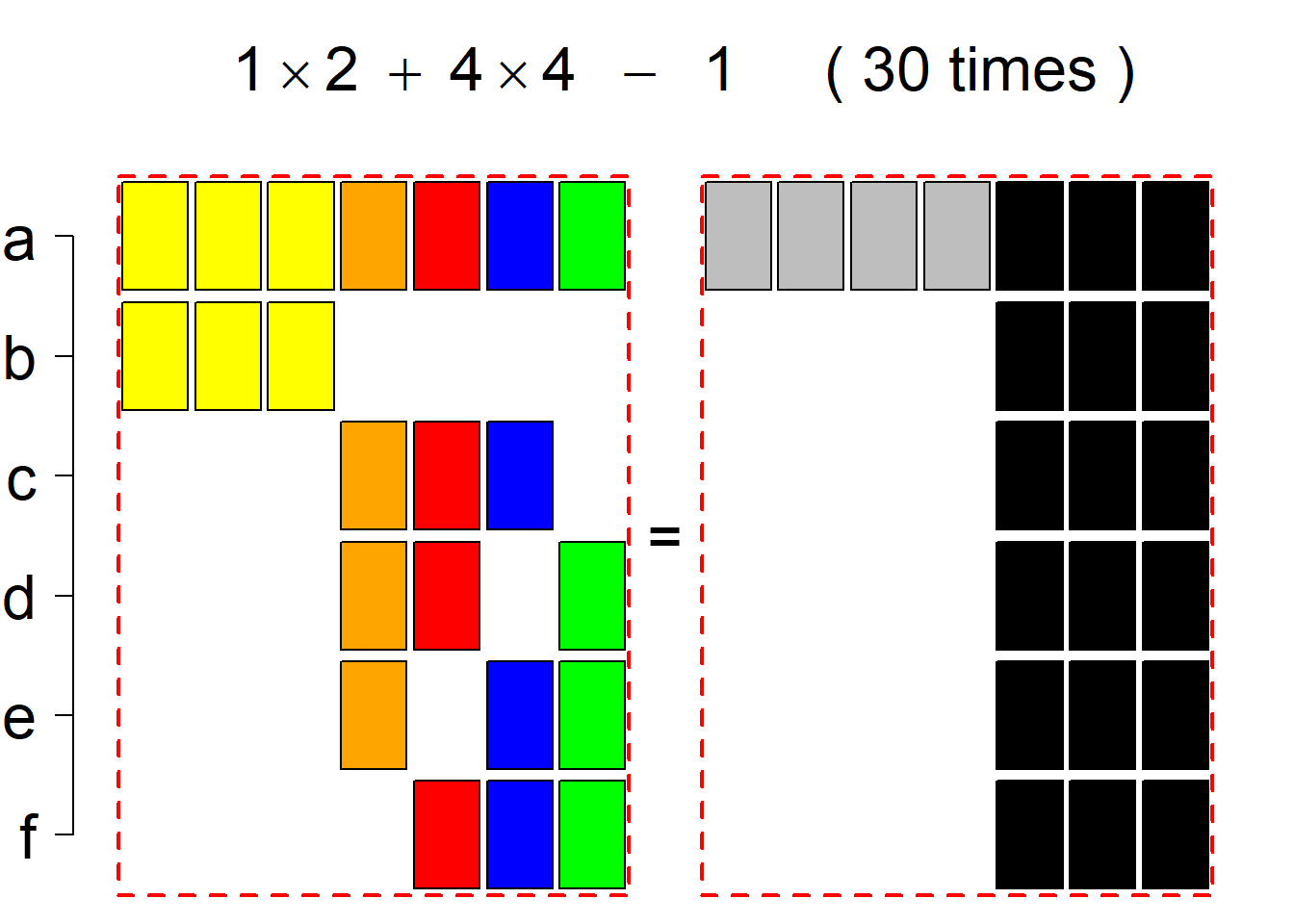
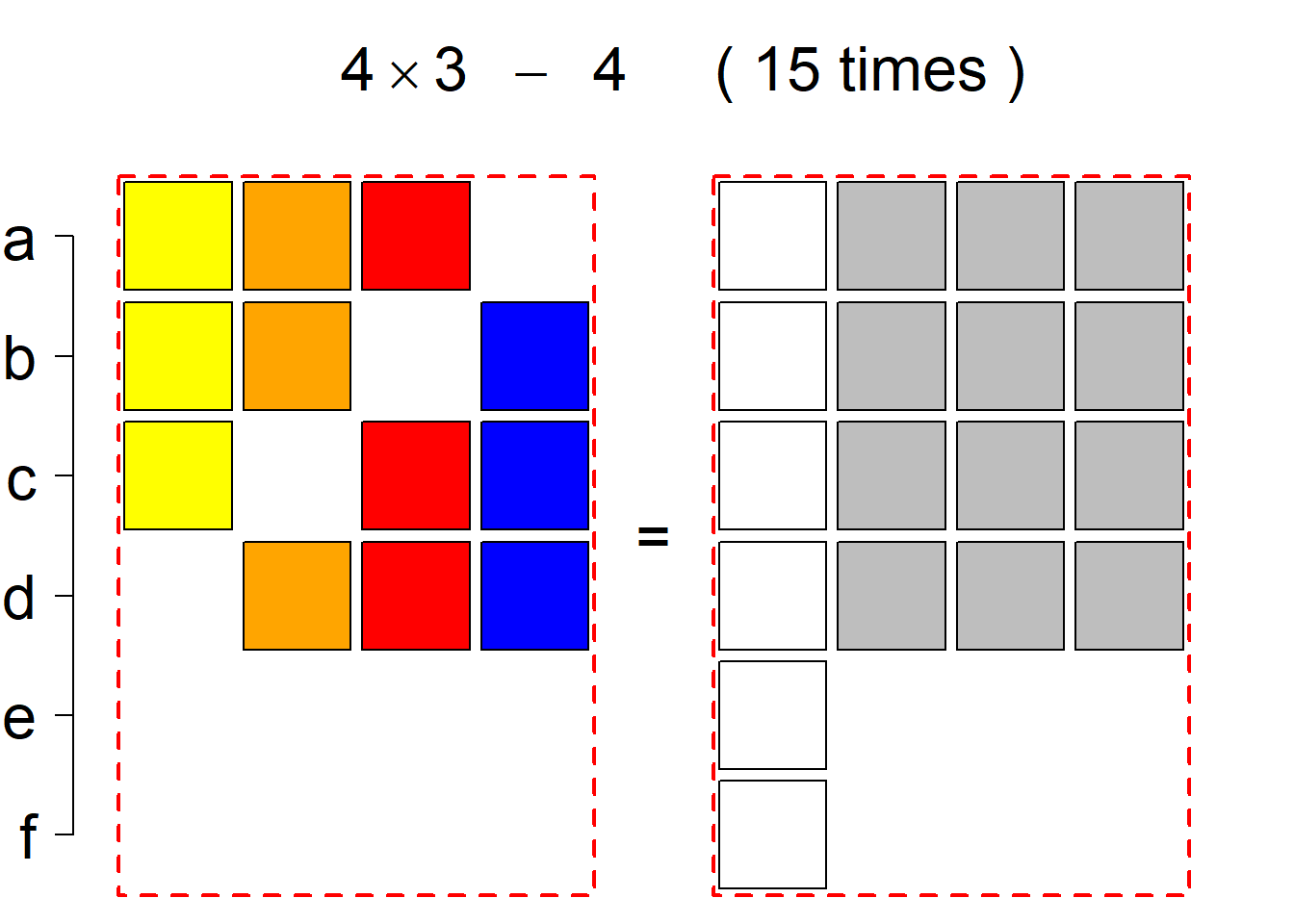
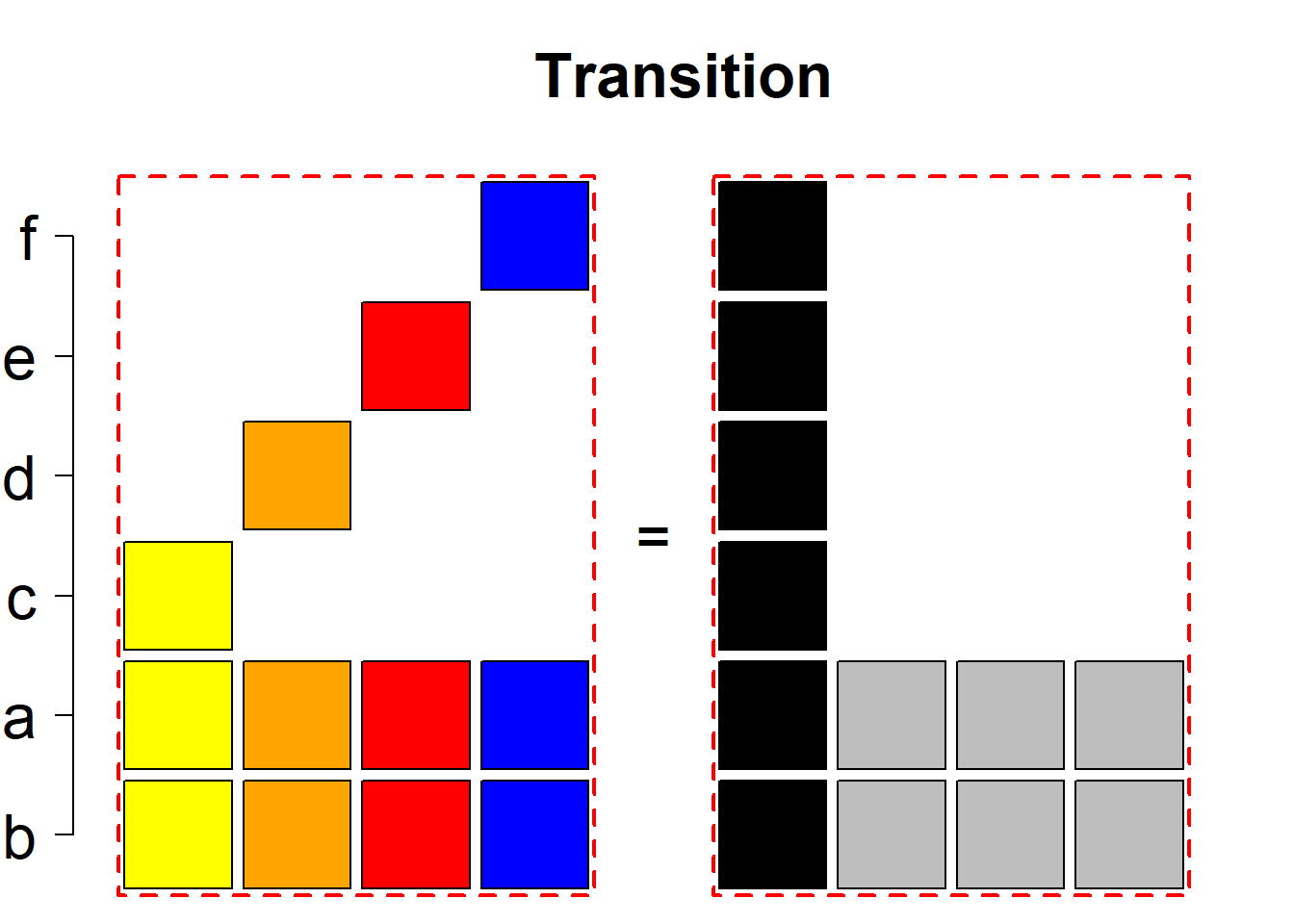
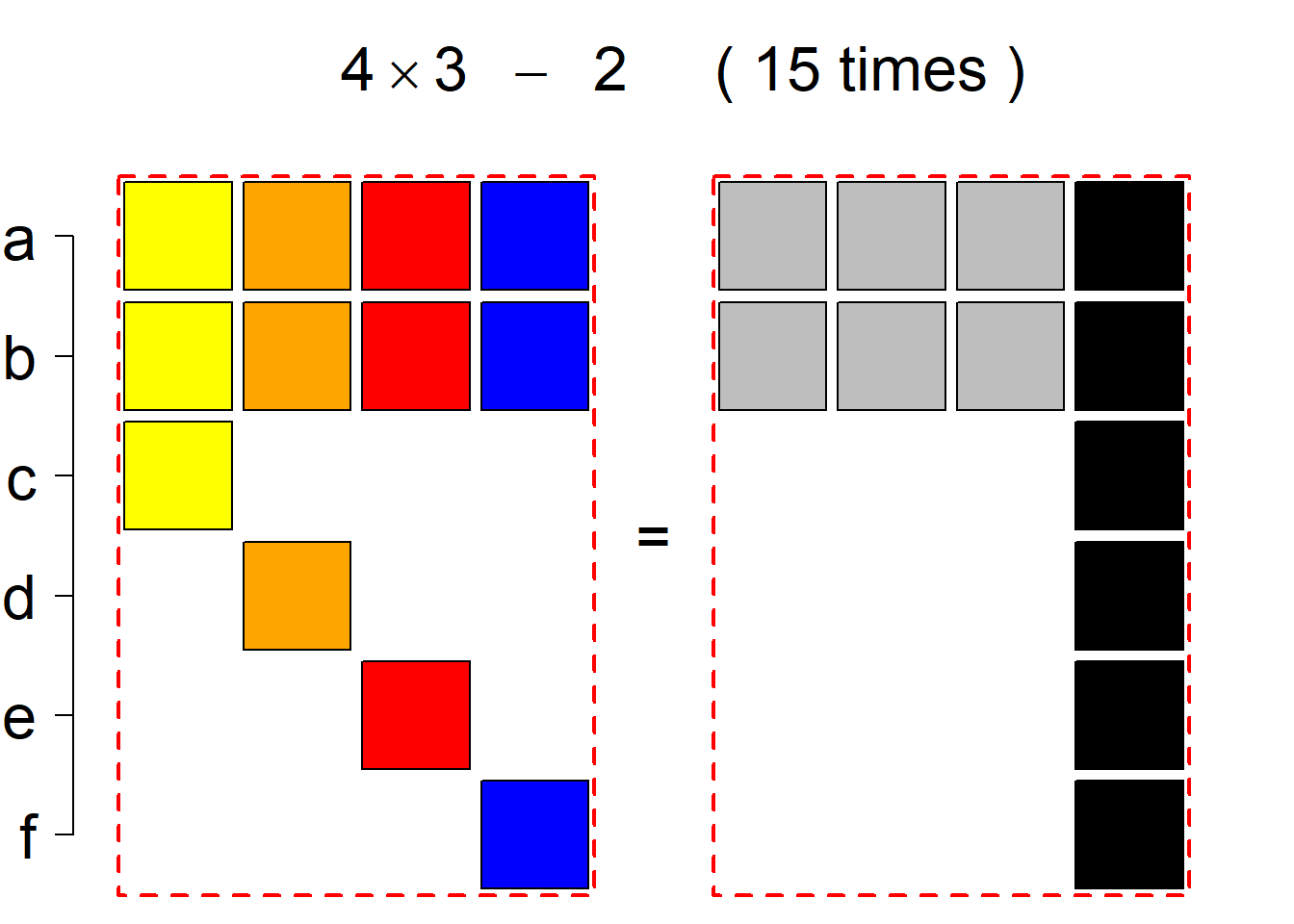
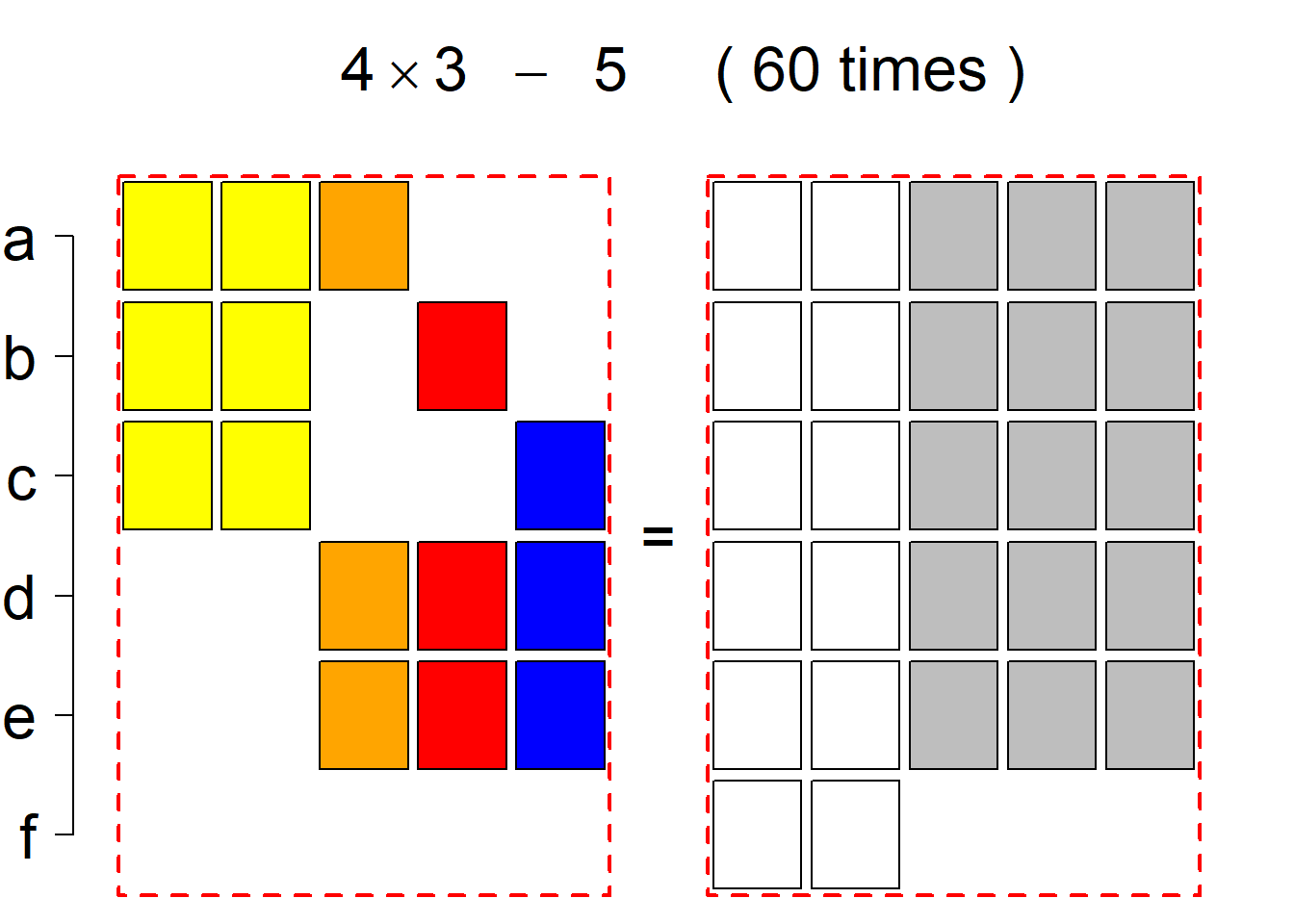
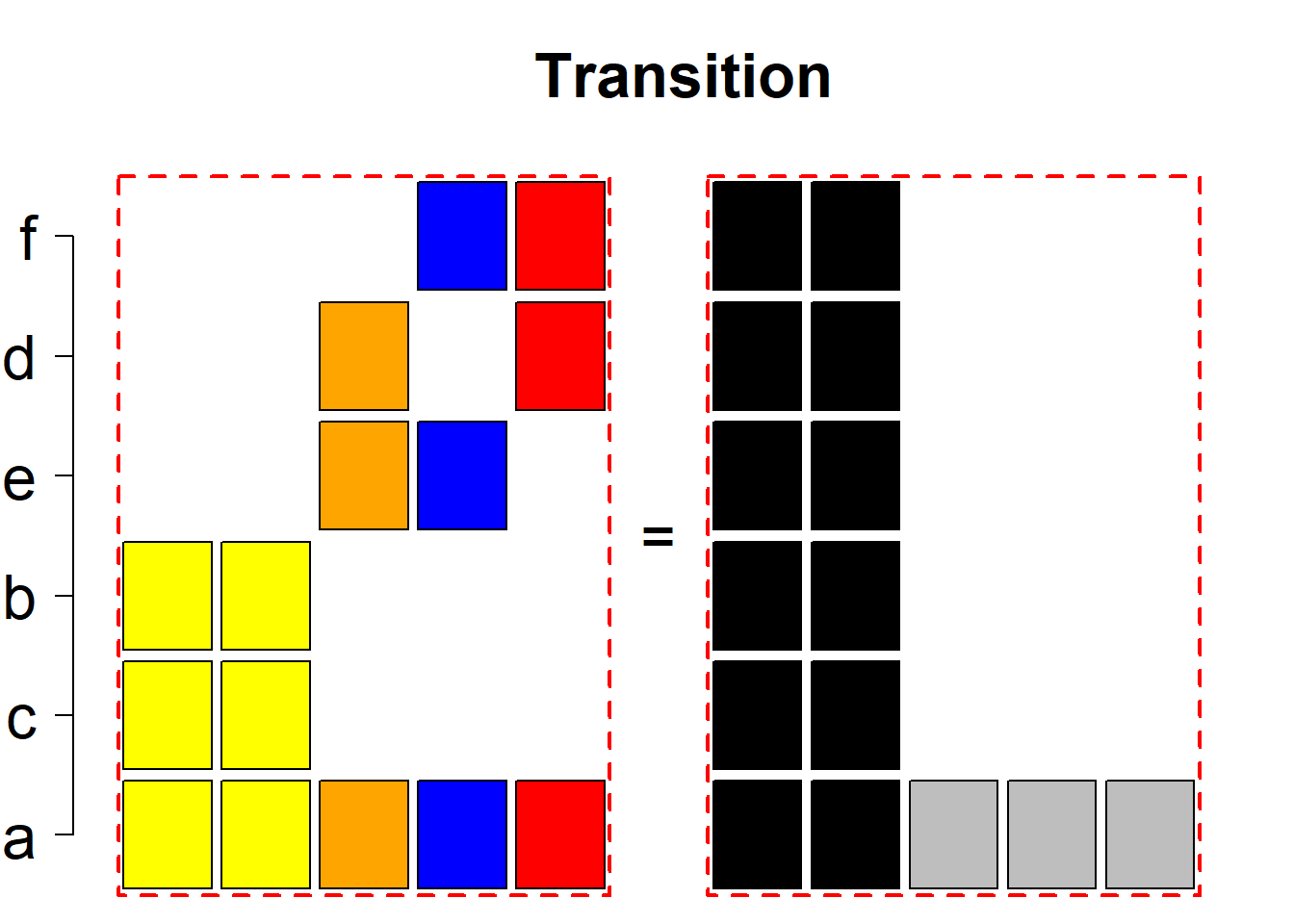
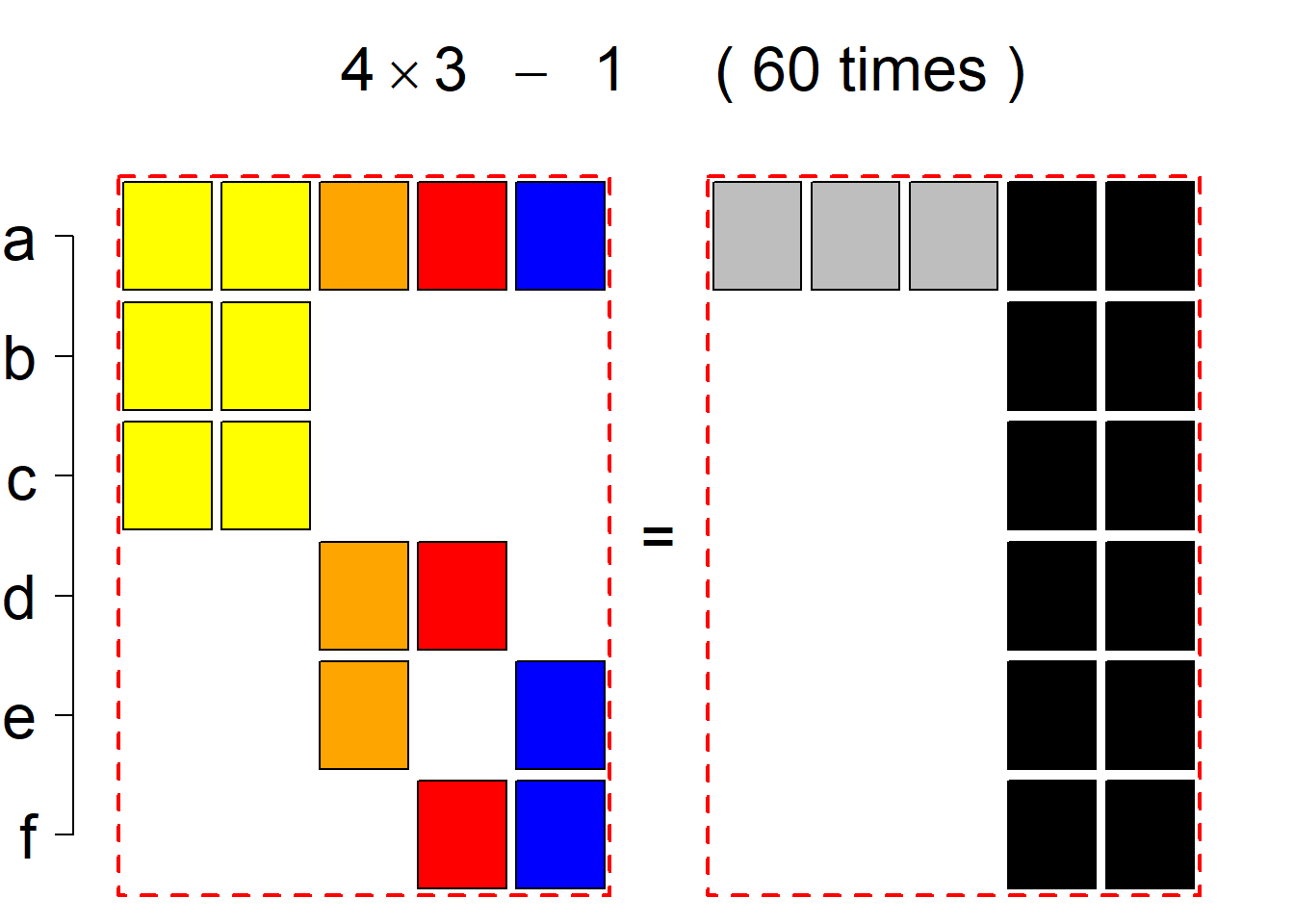
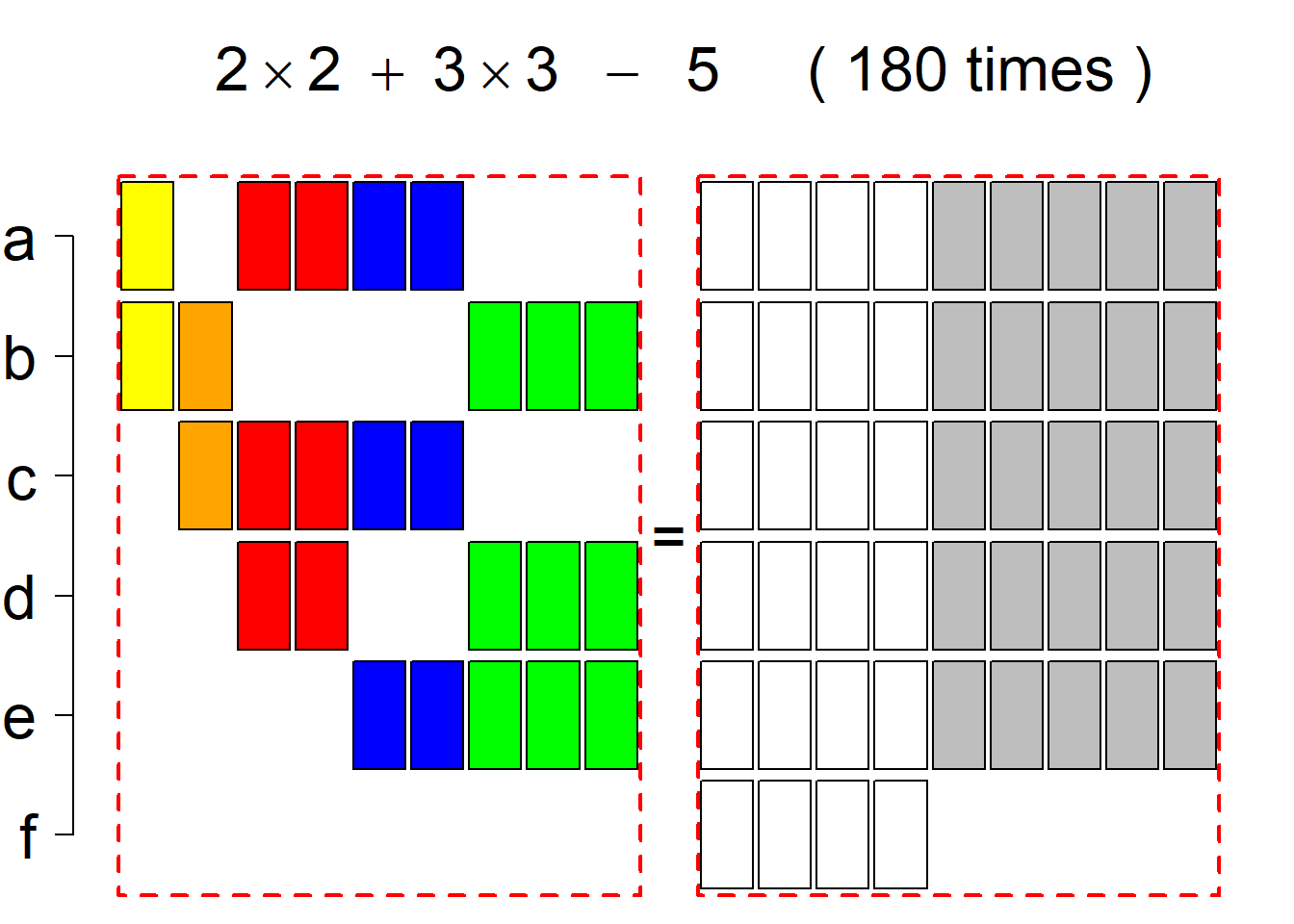
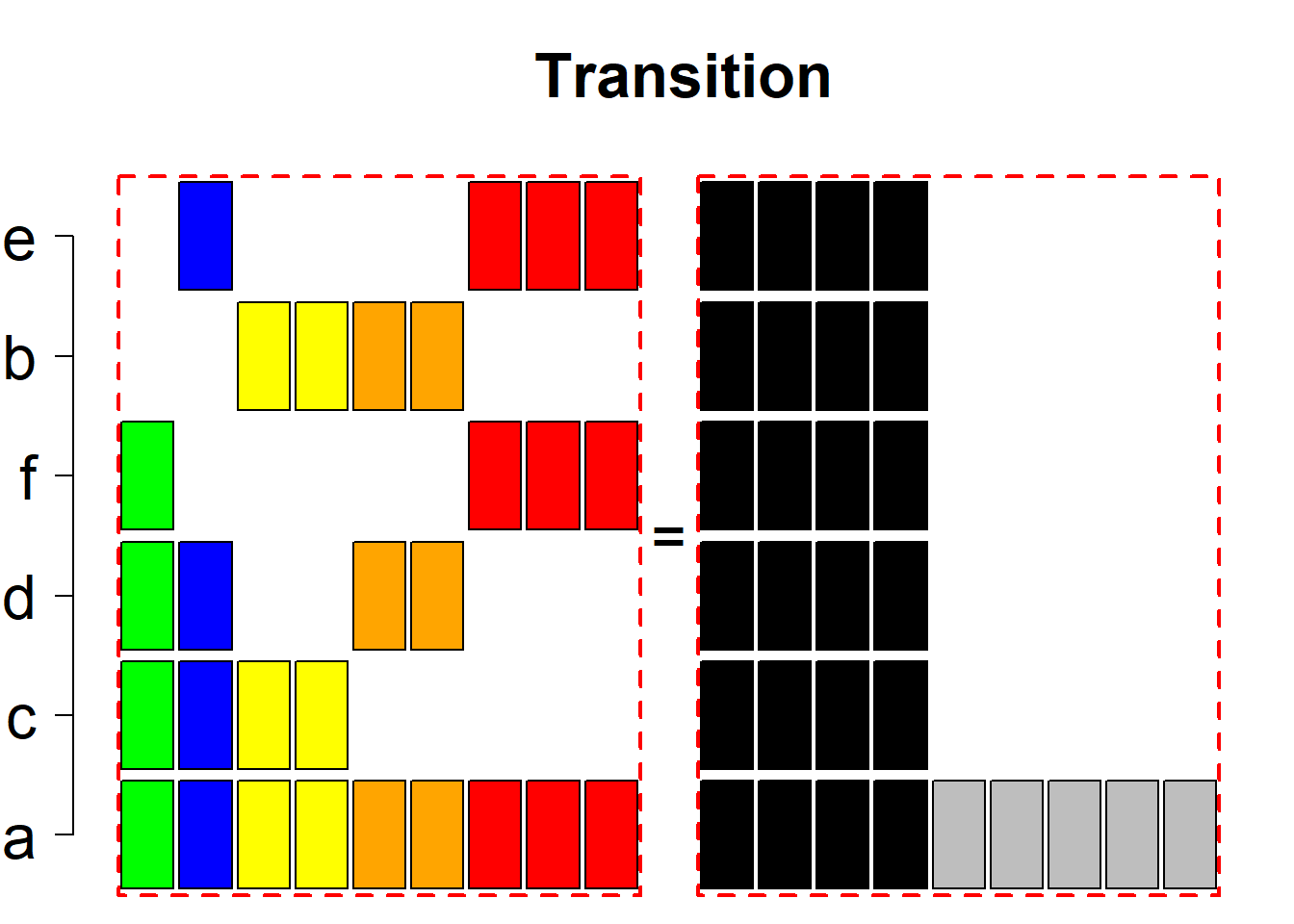
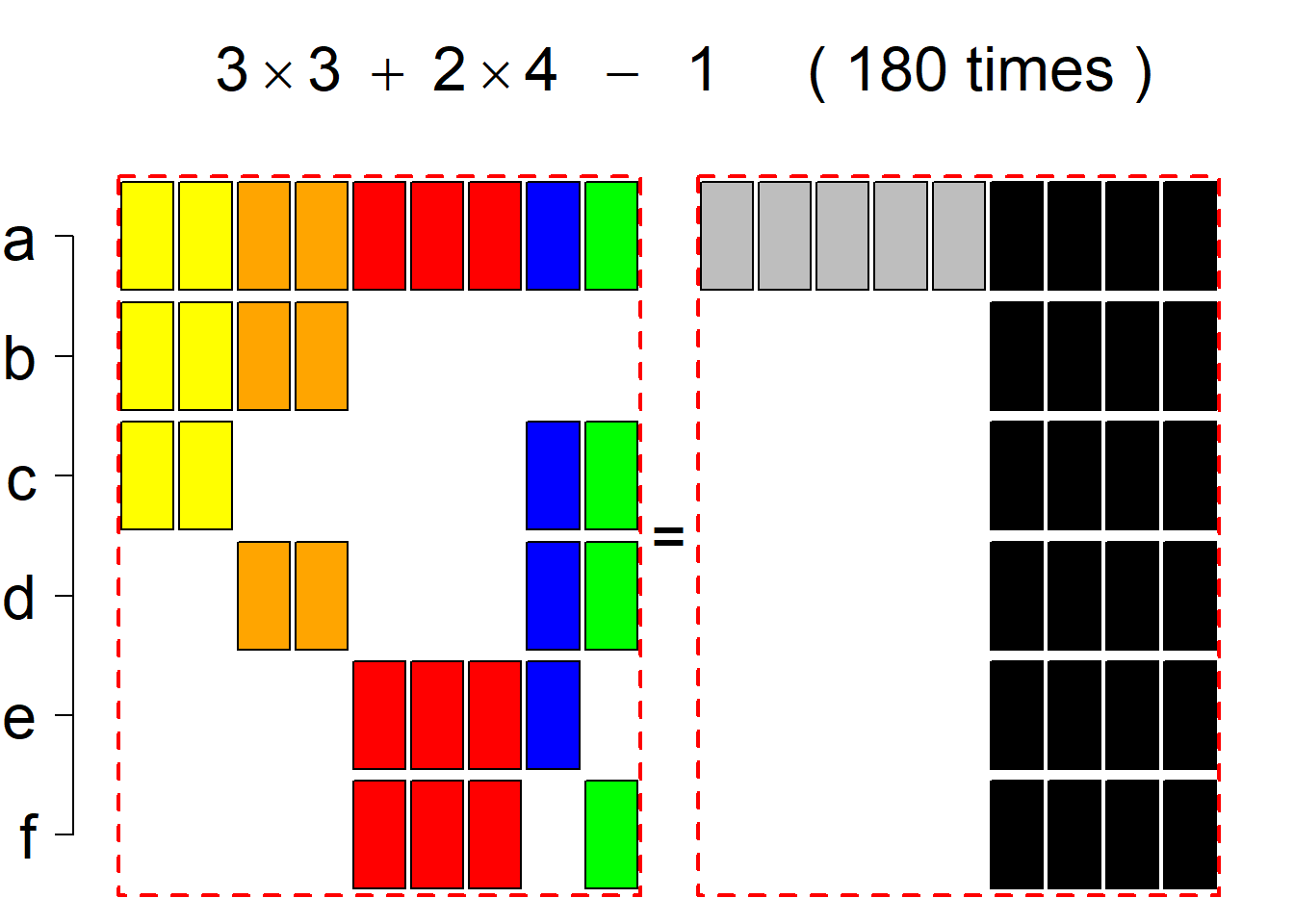
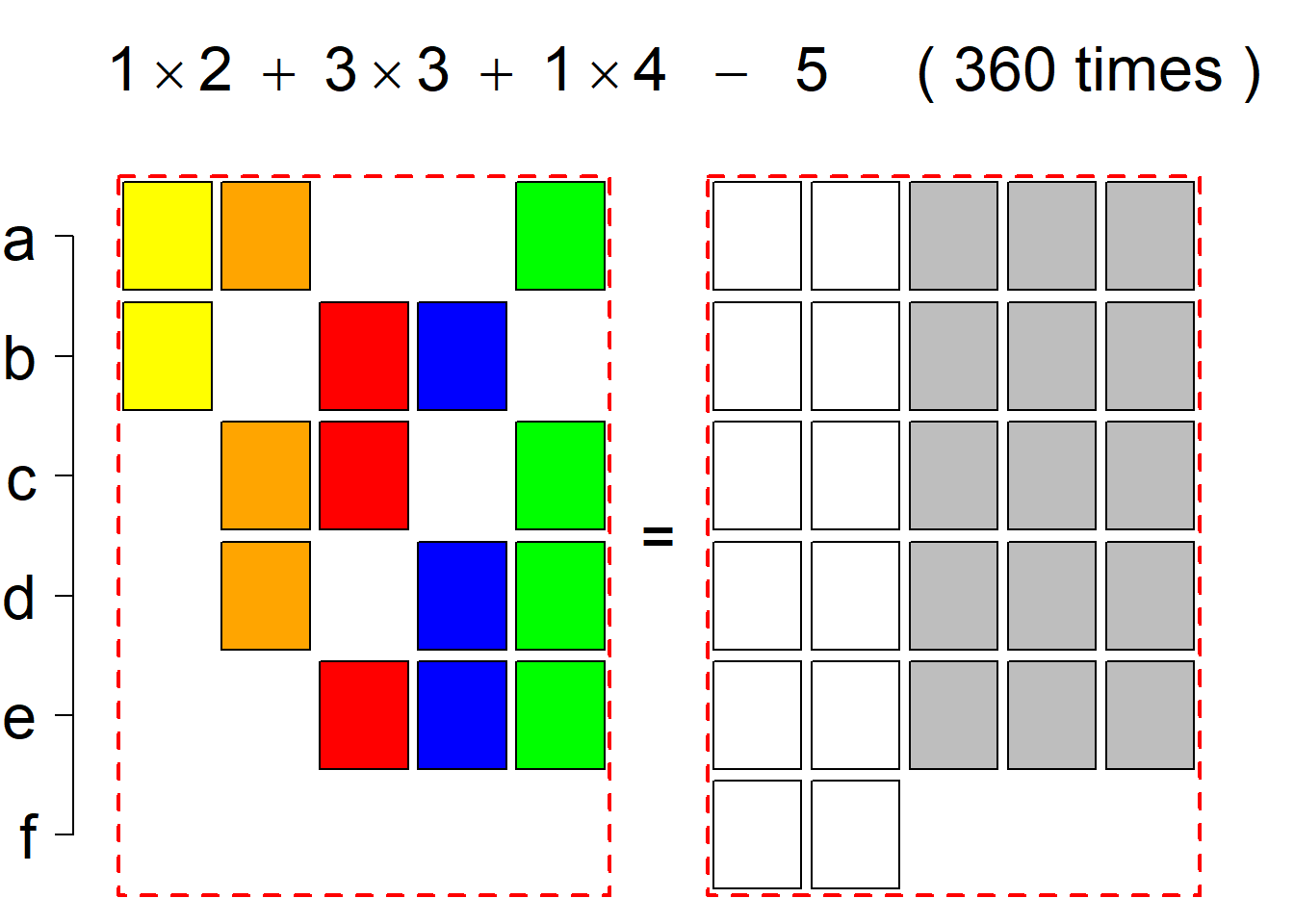
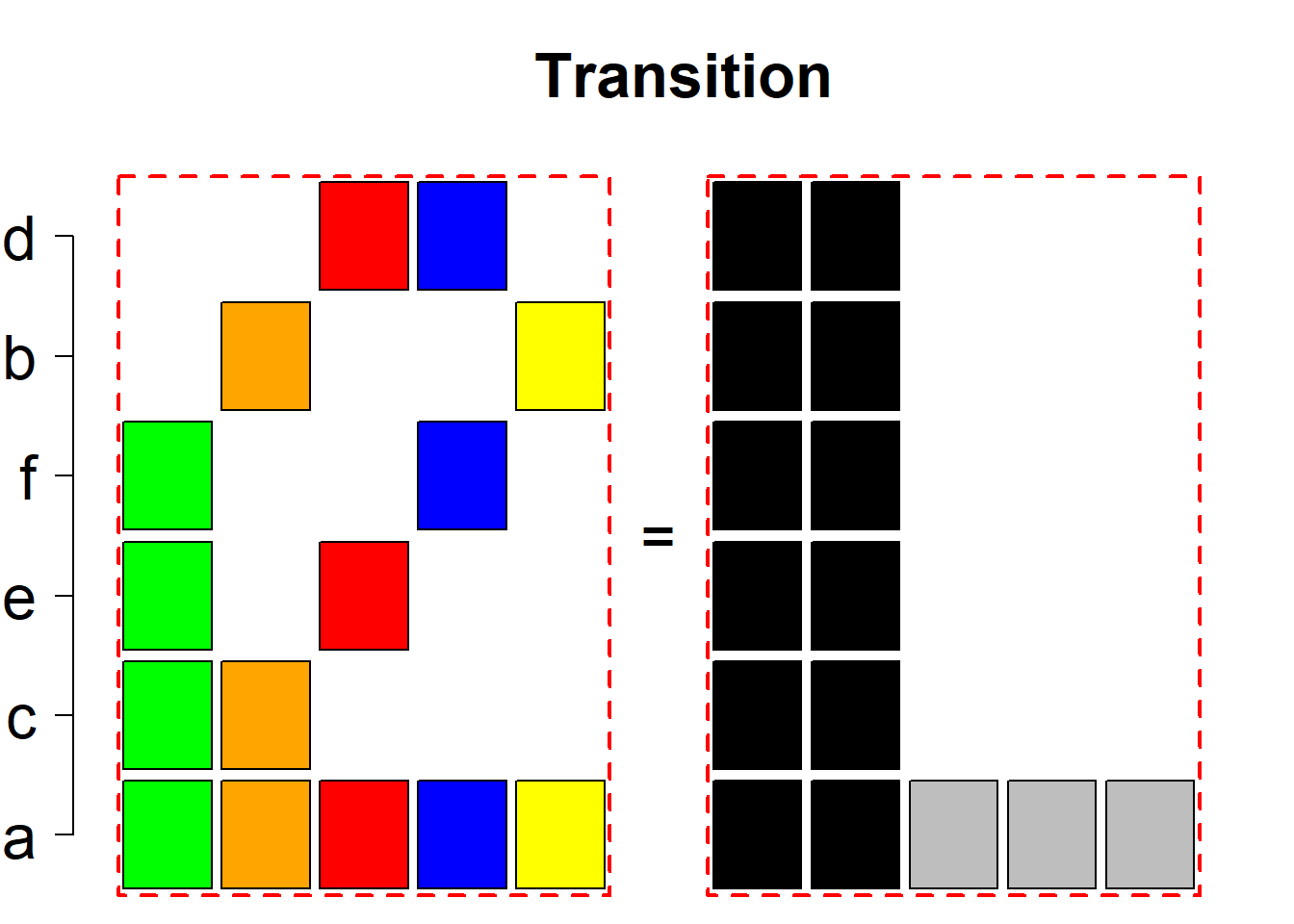
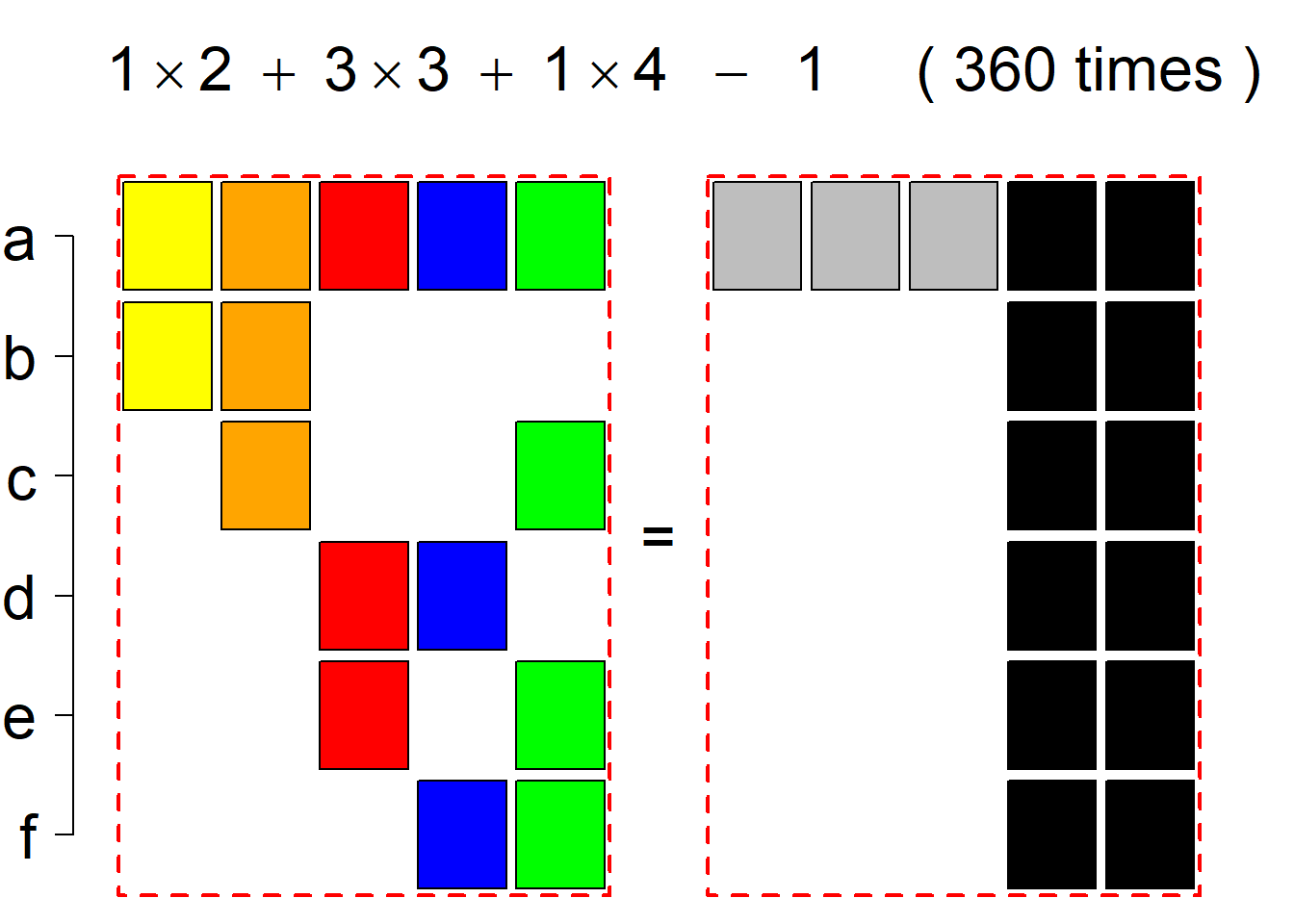
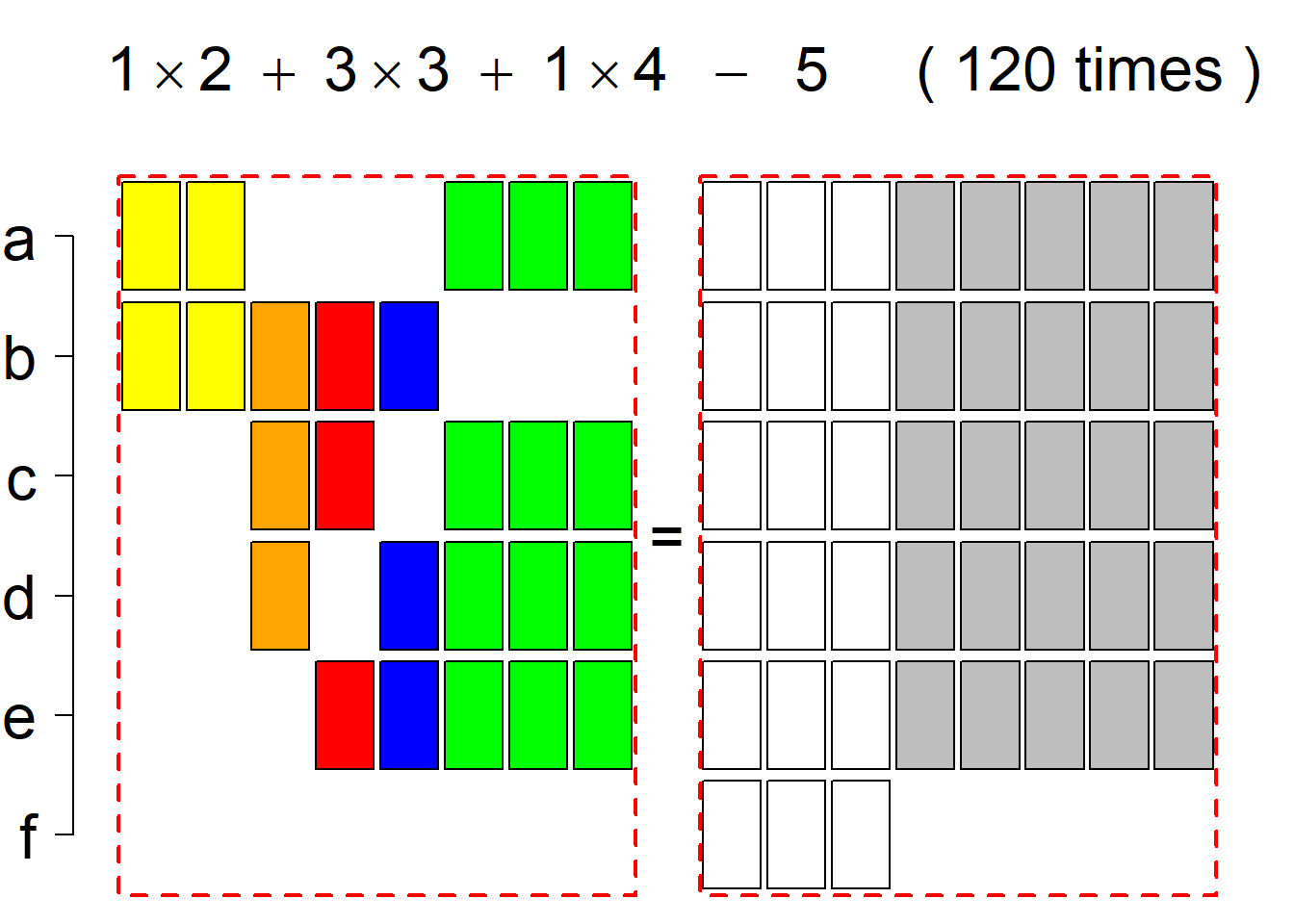
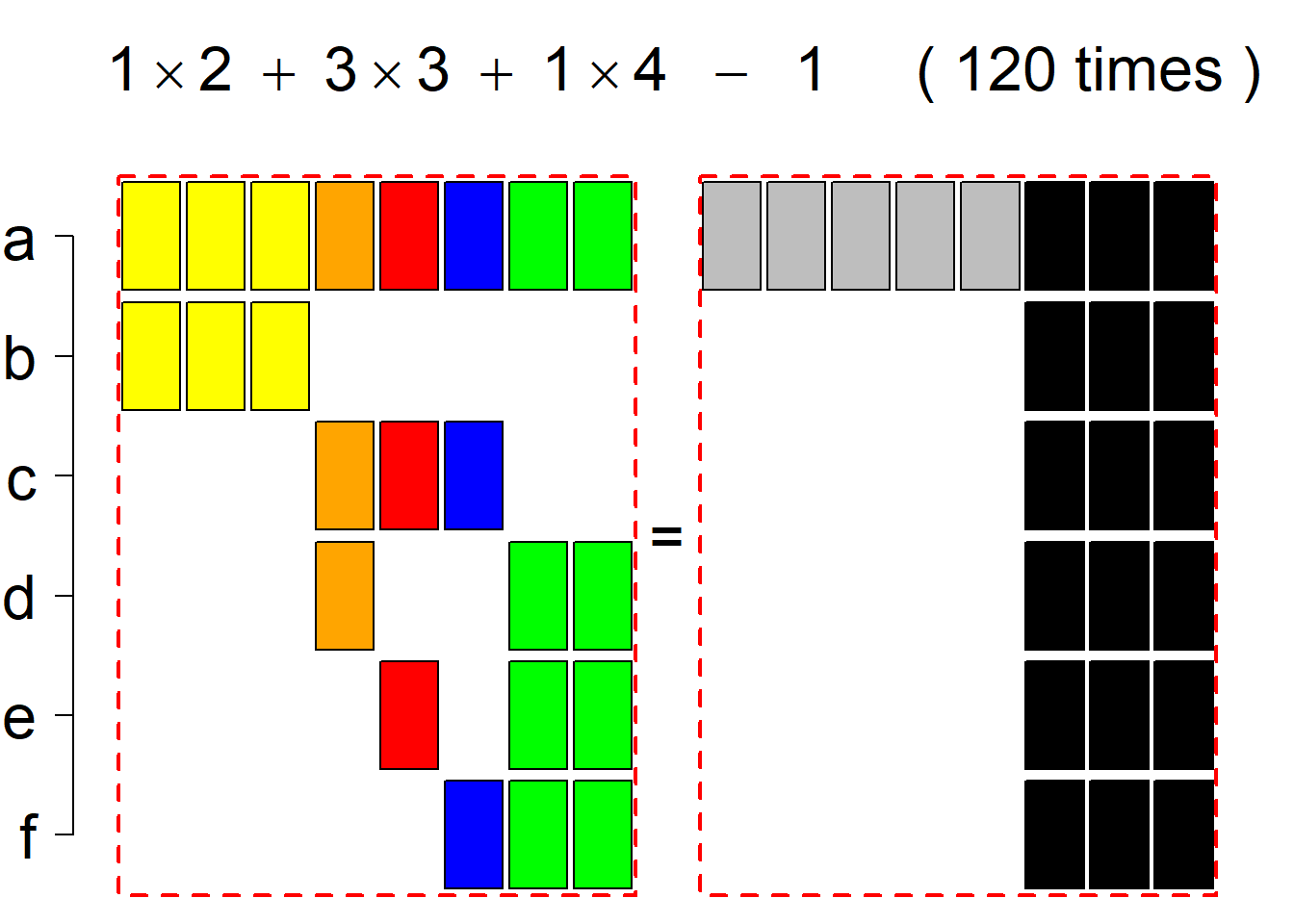
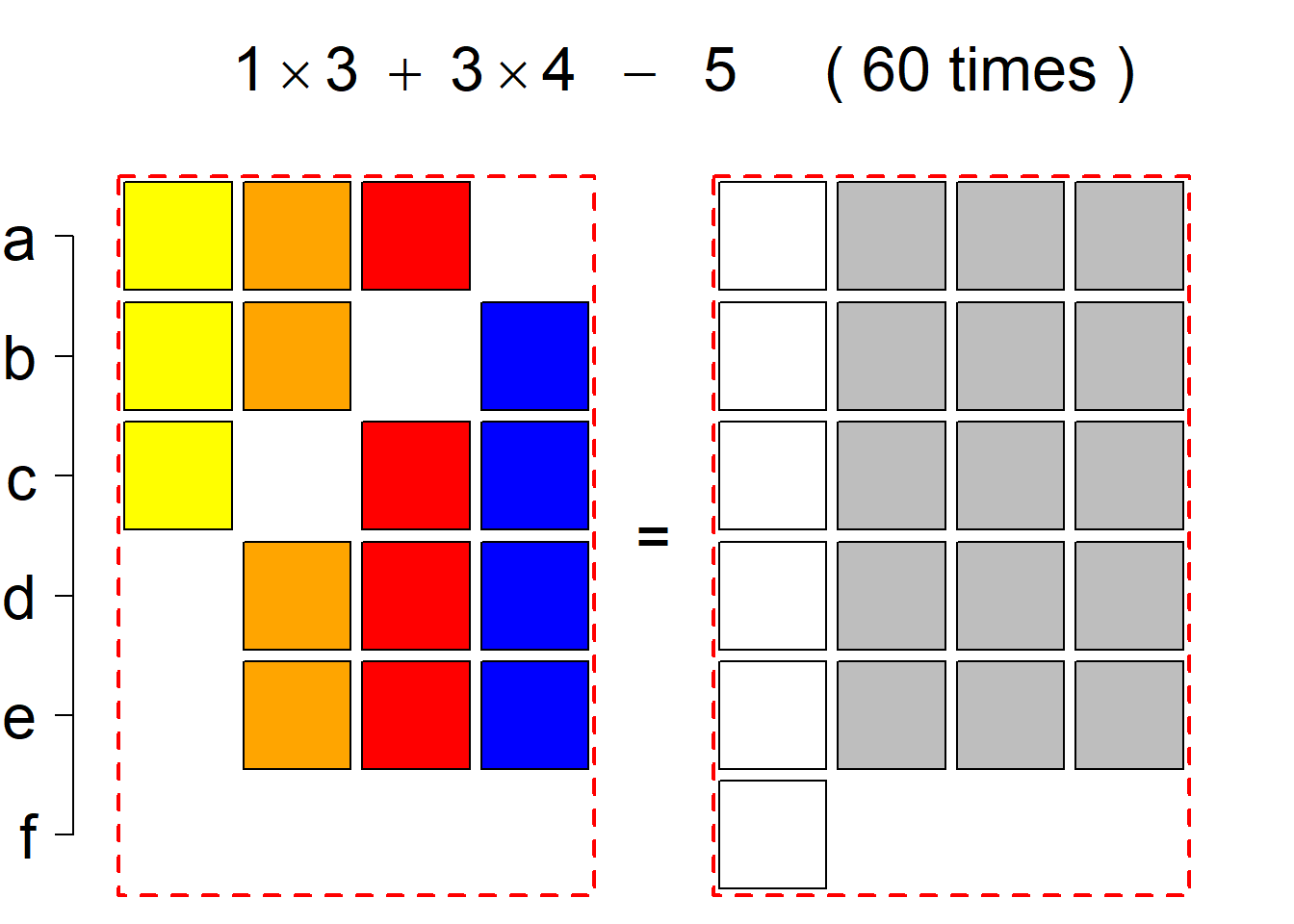
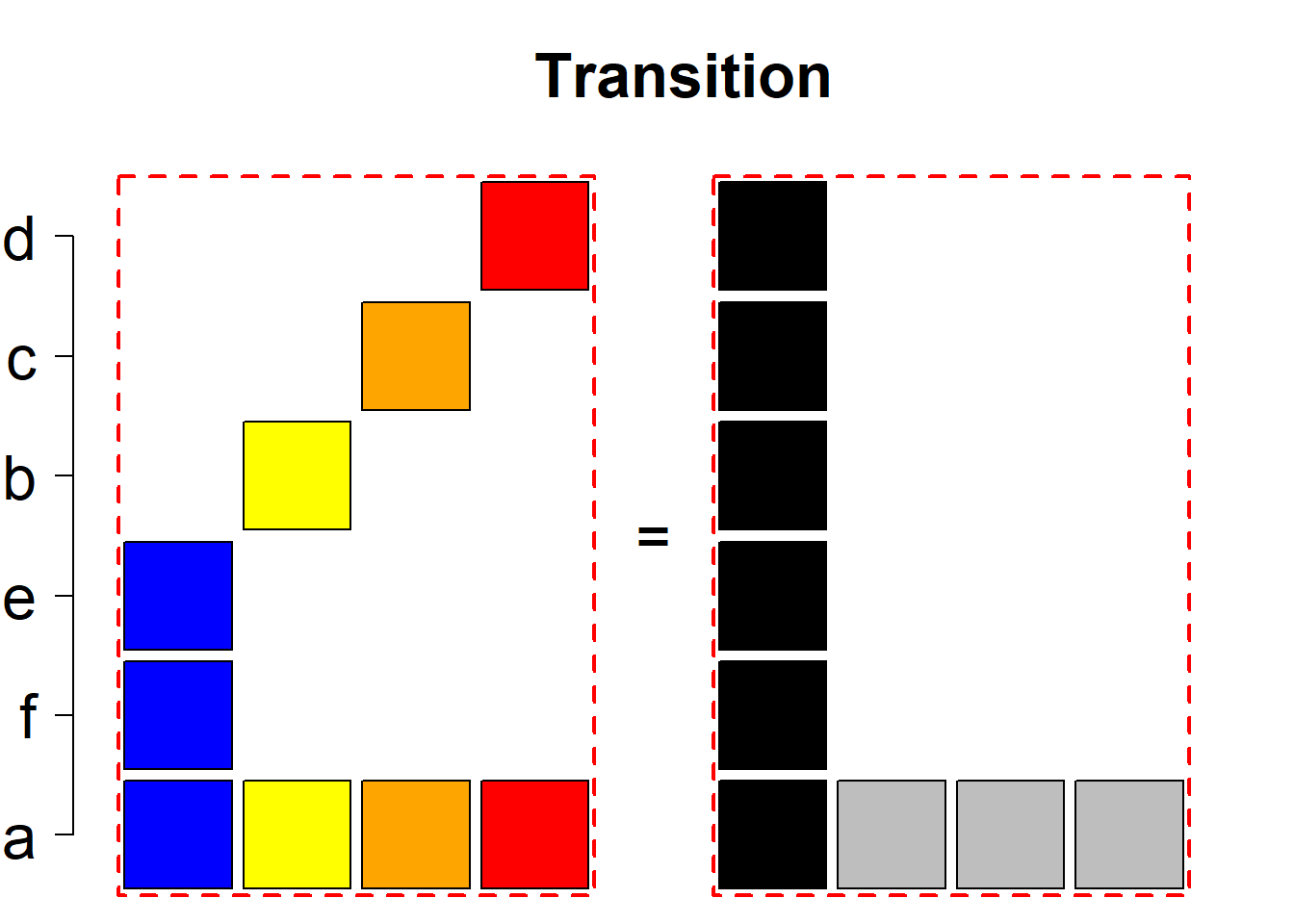

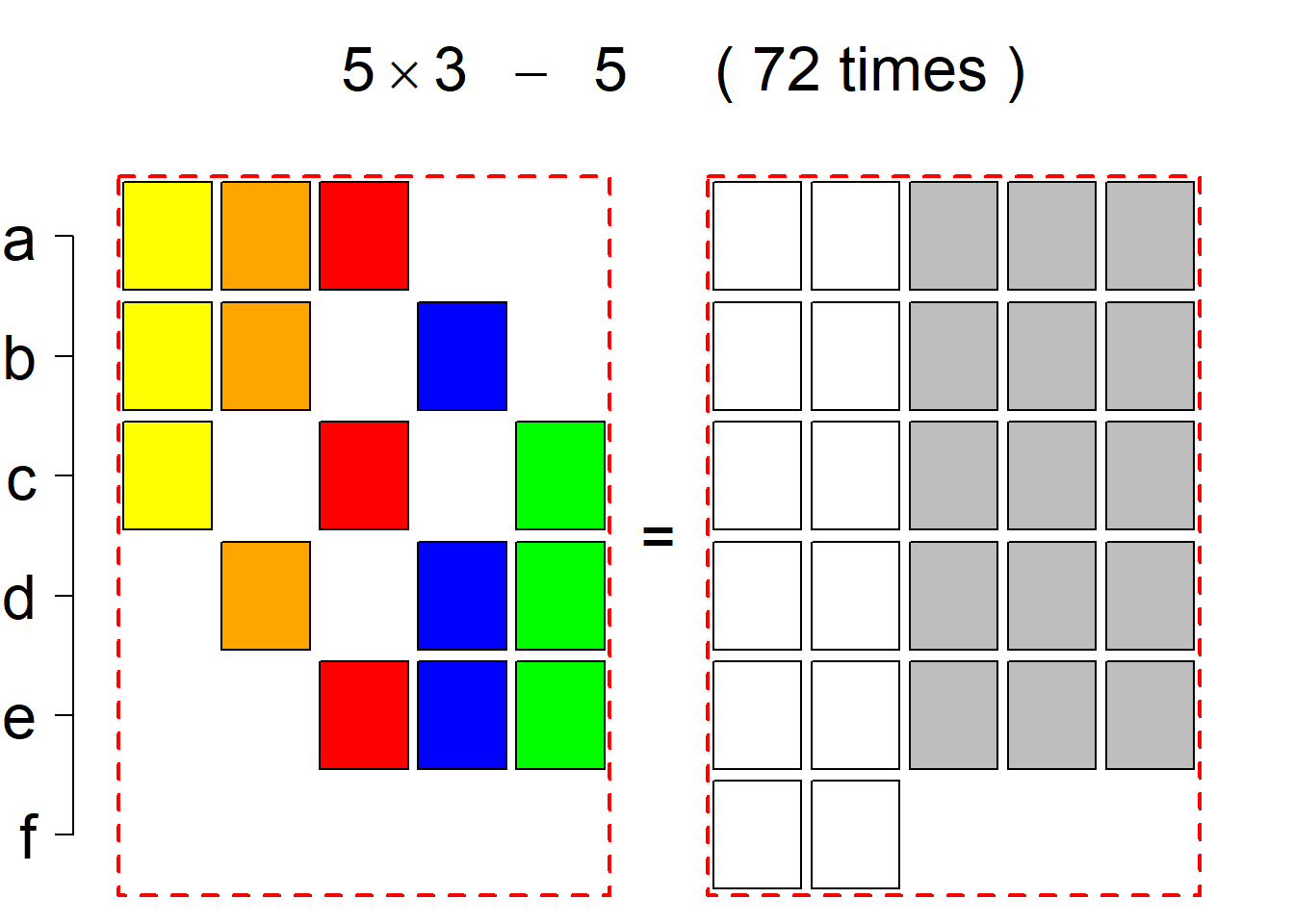
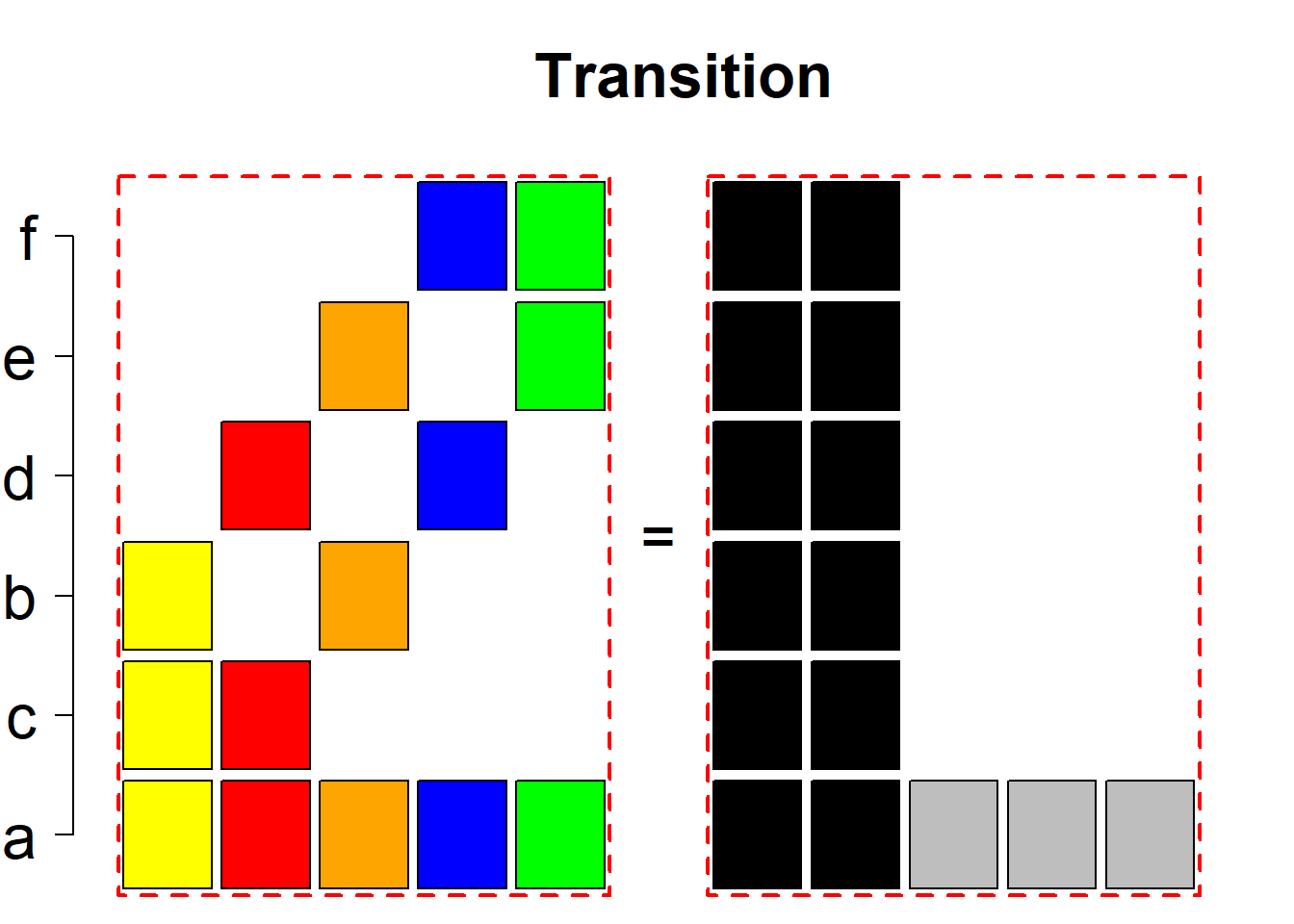
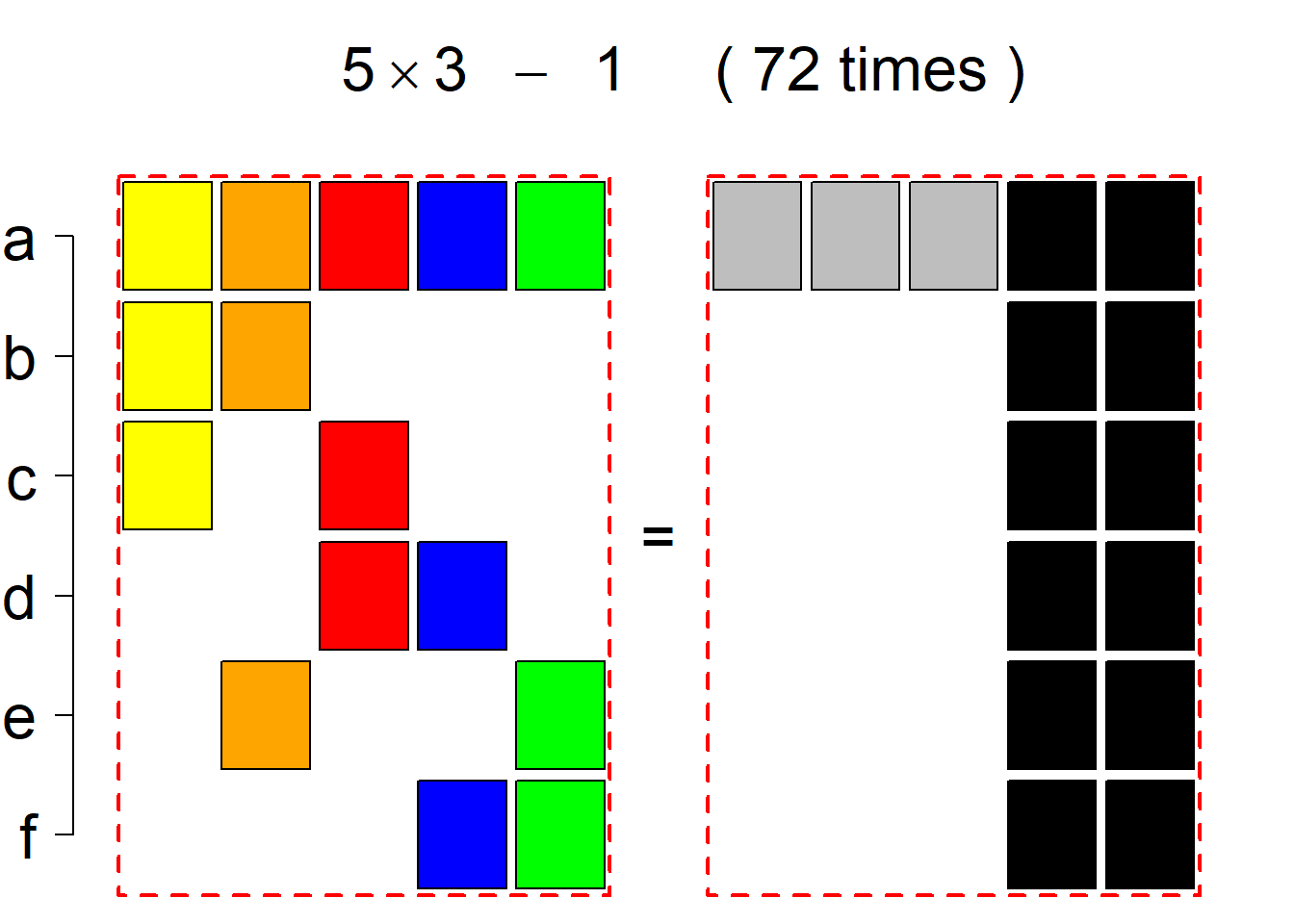
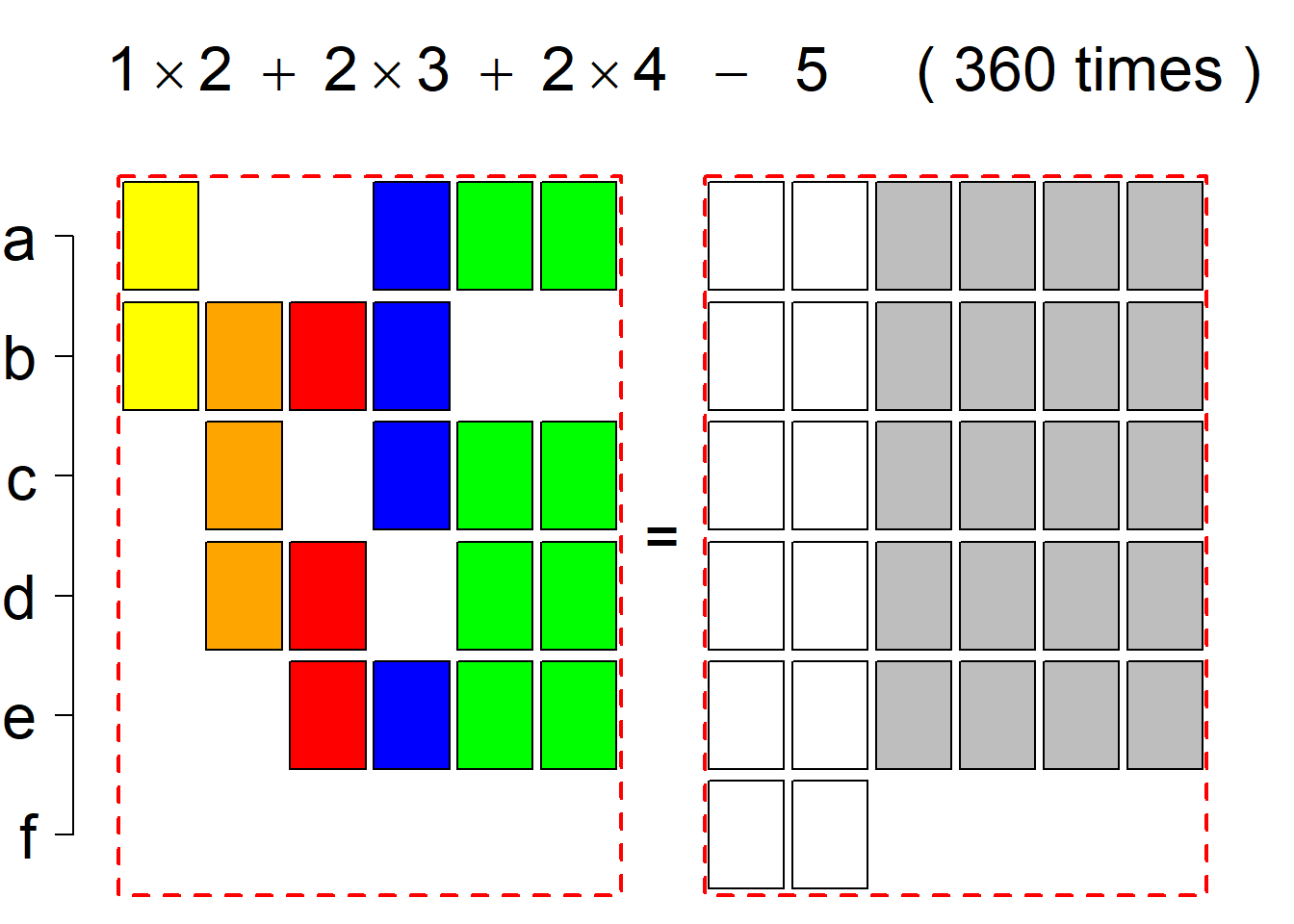
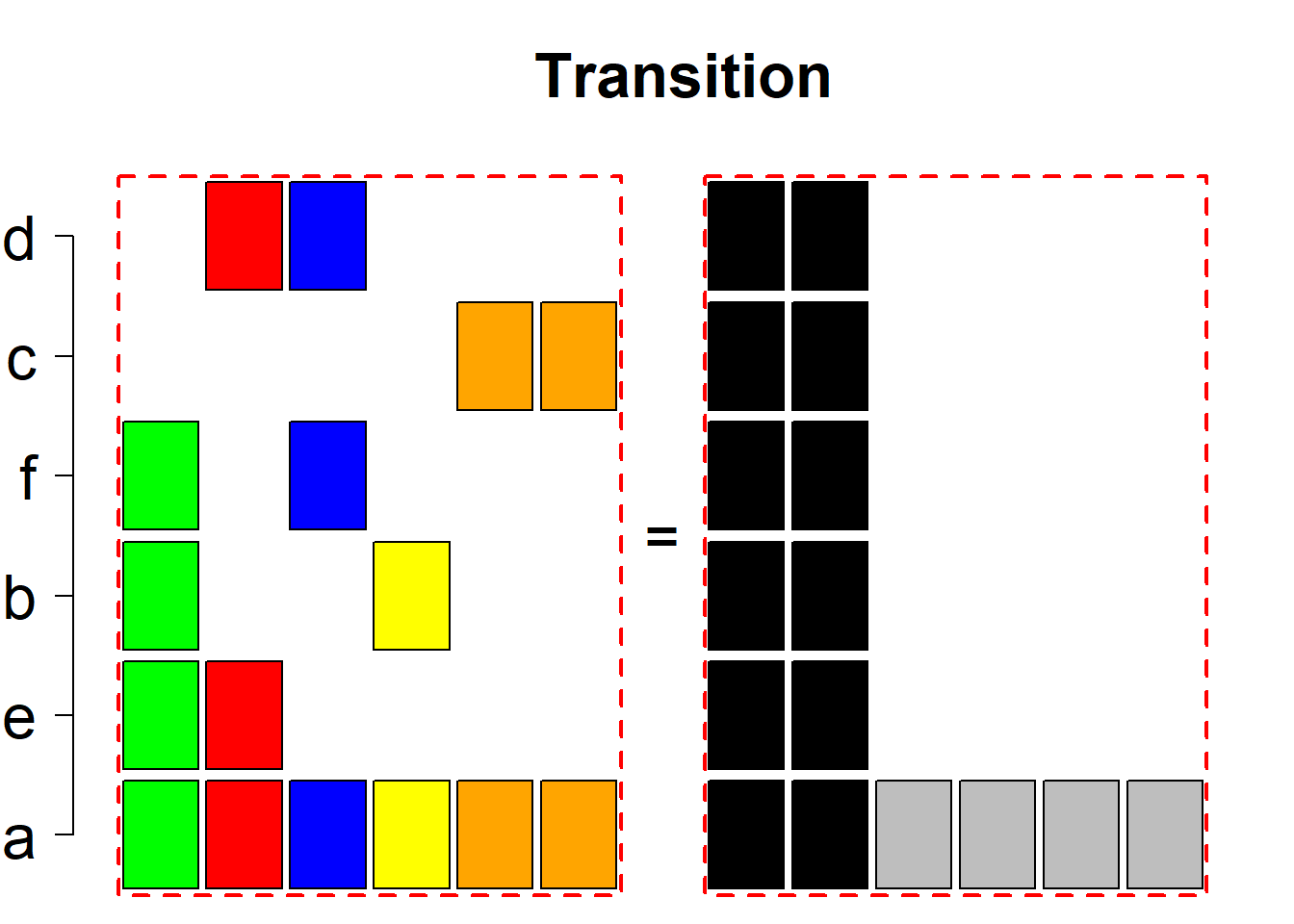


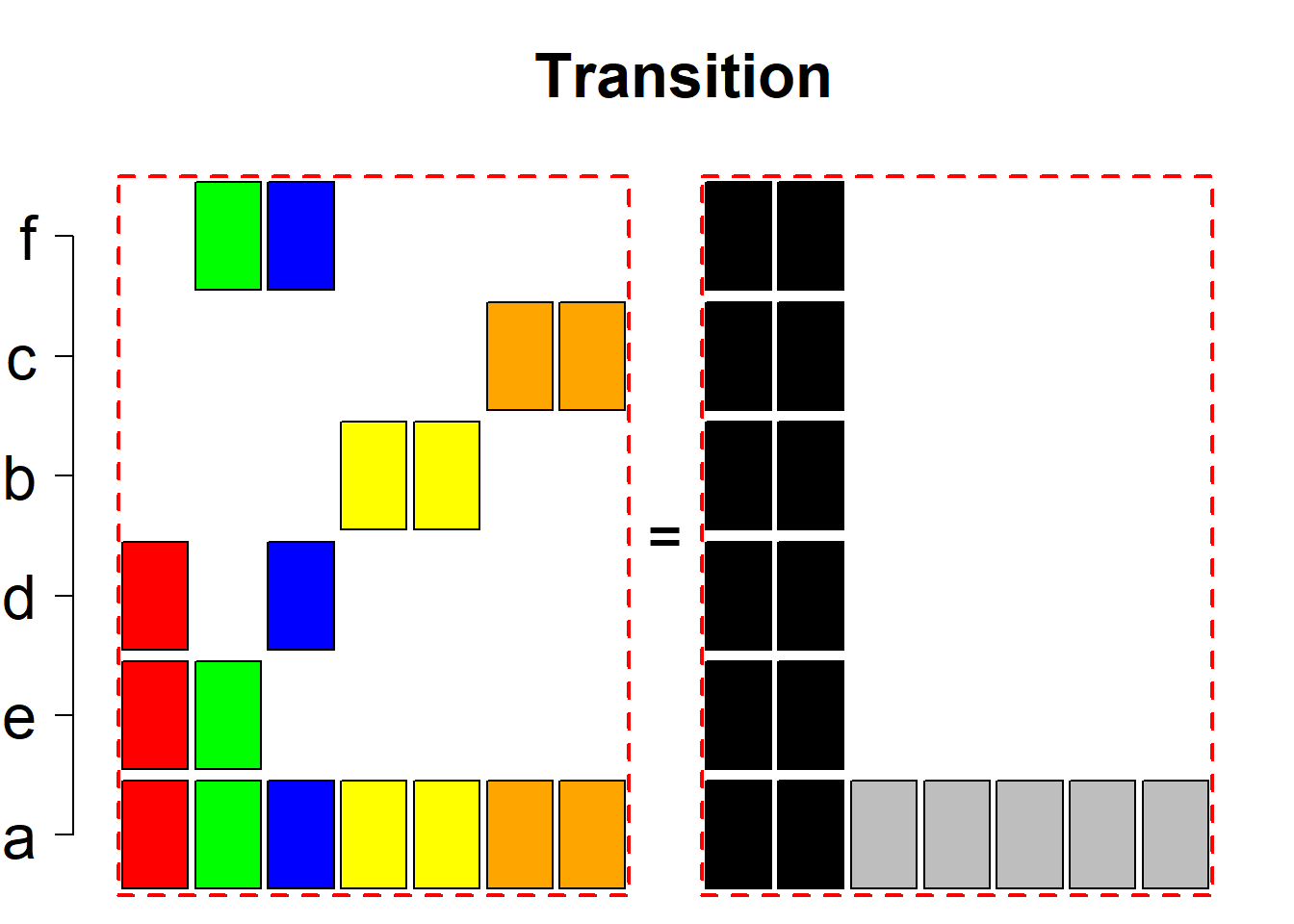
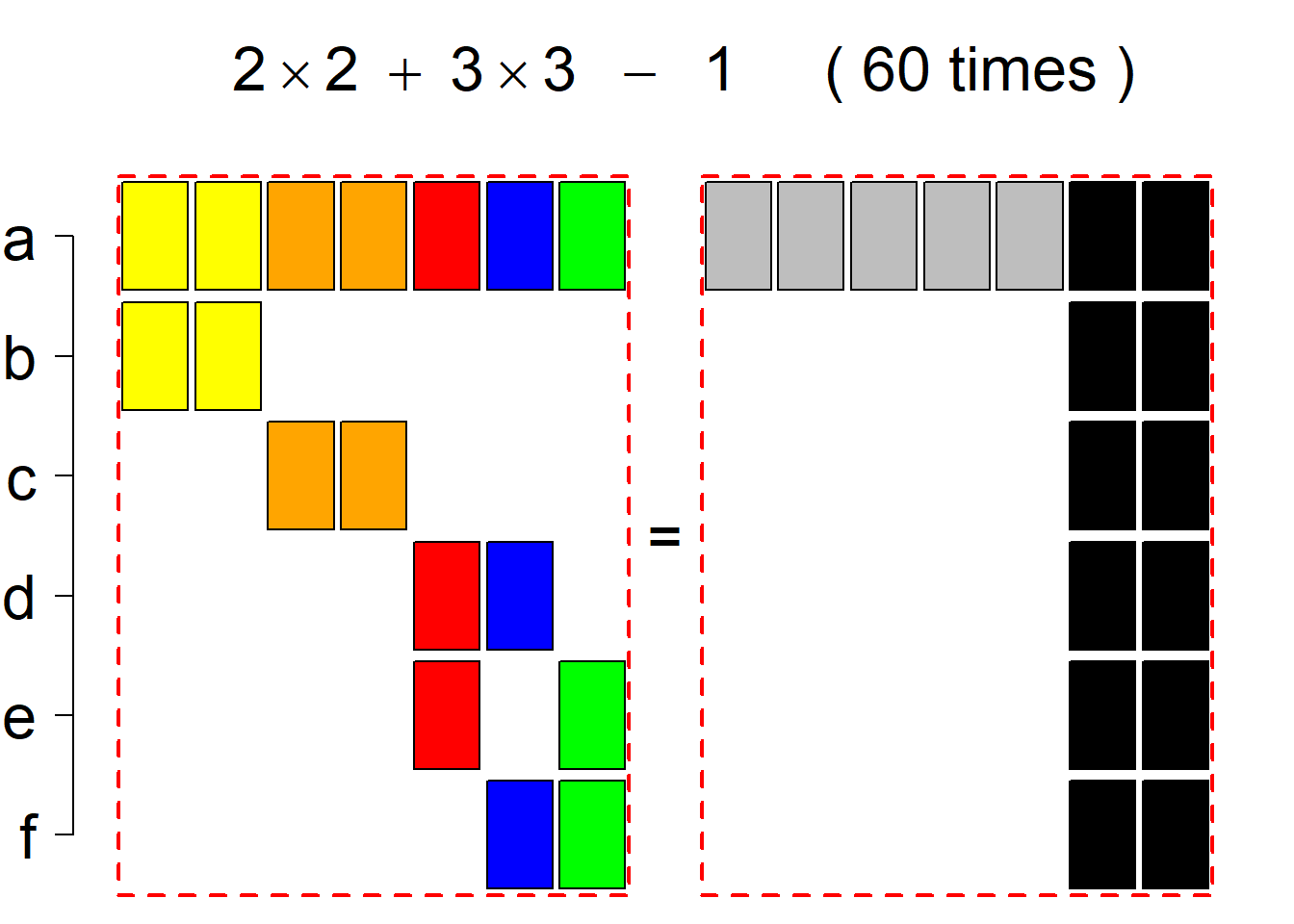
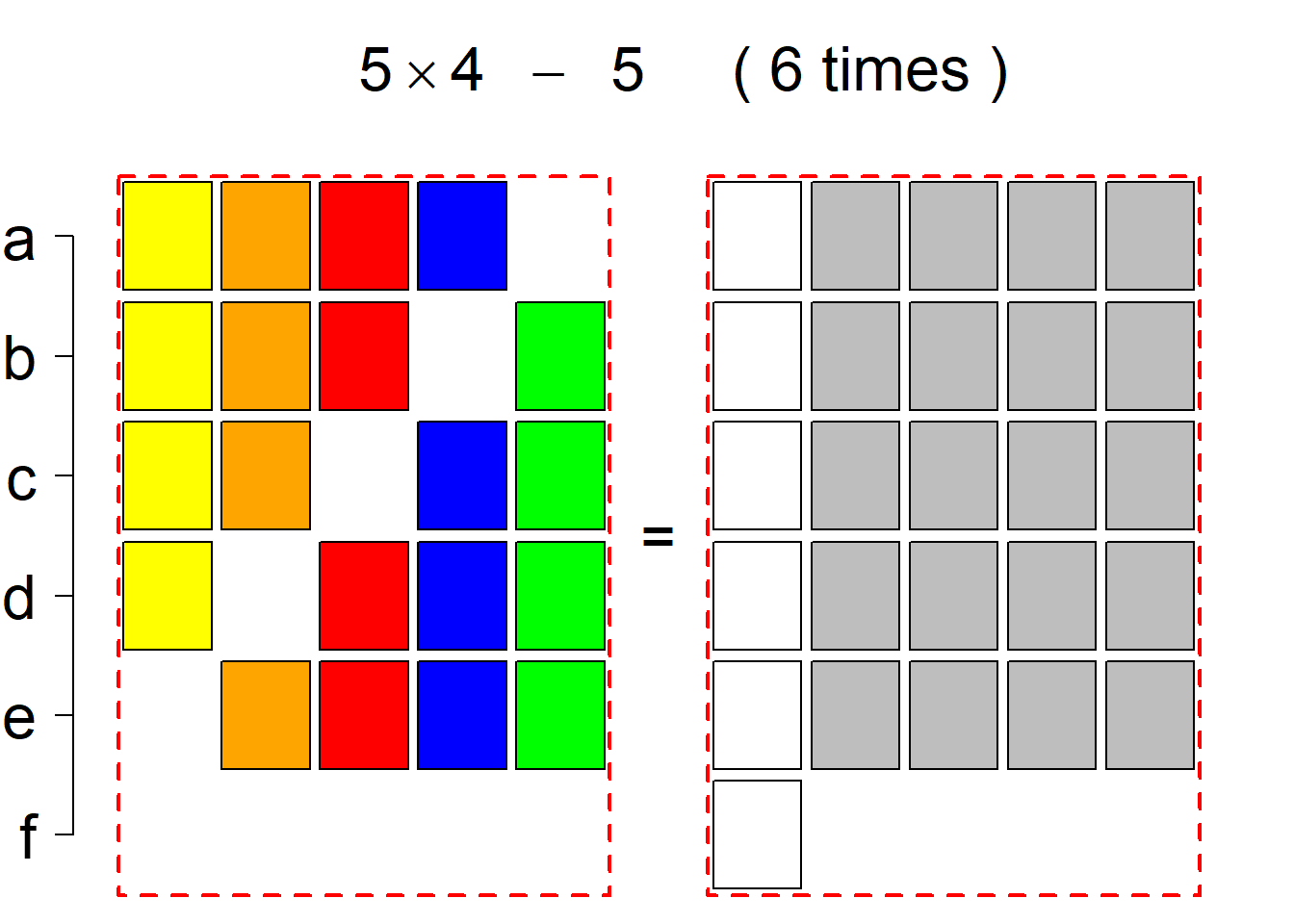
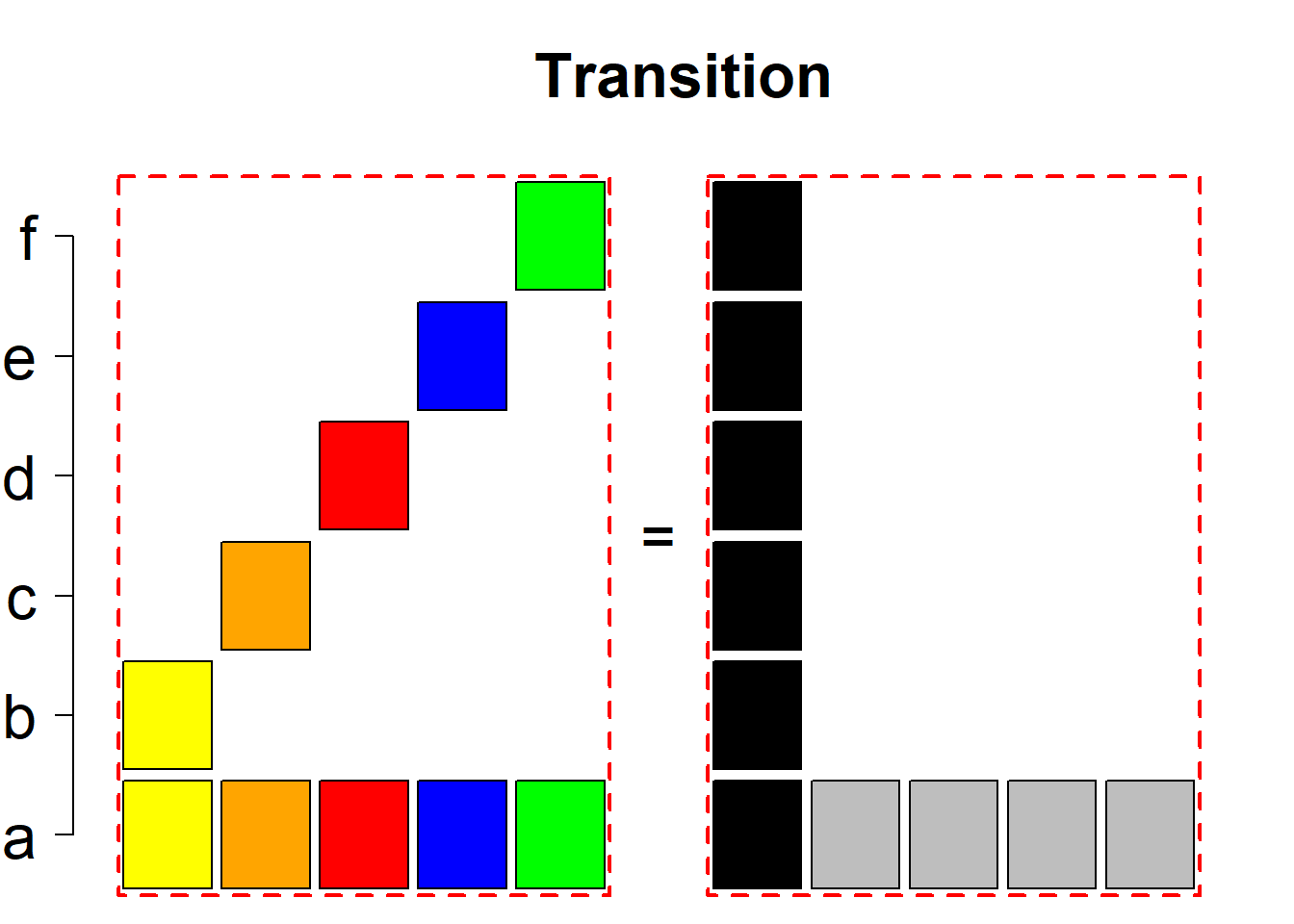
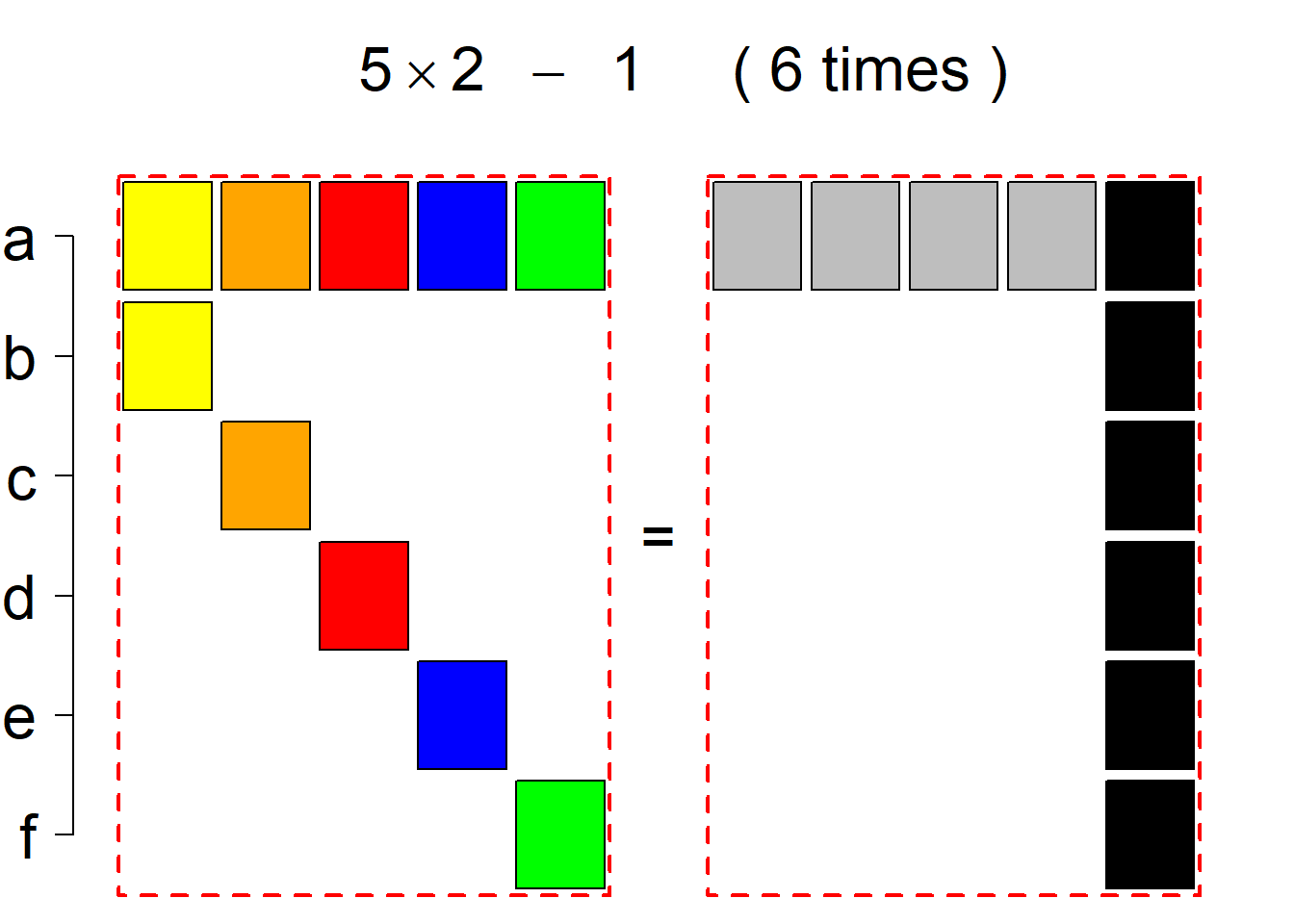
The third classification class
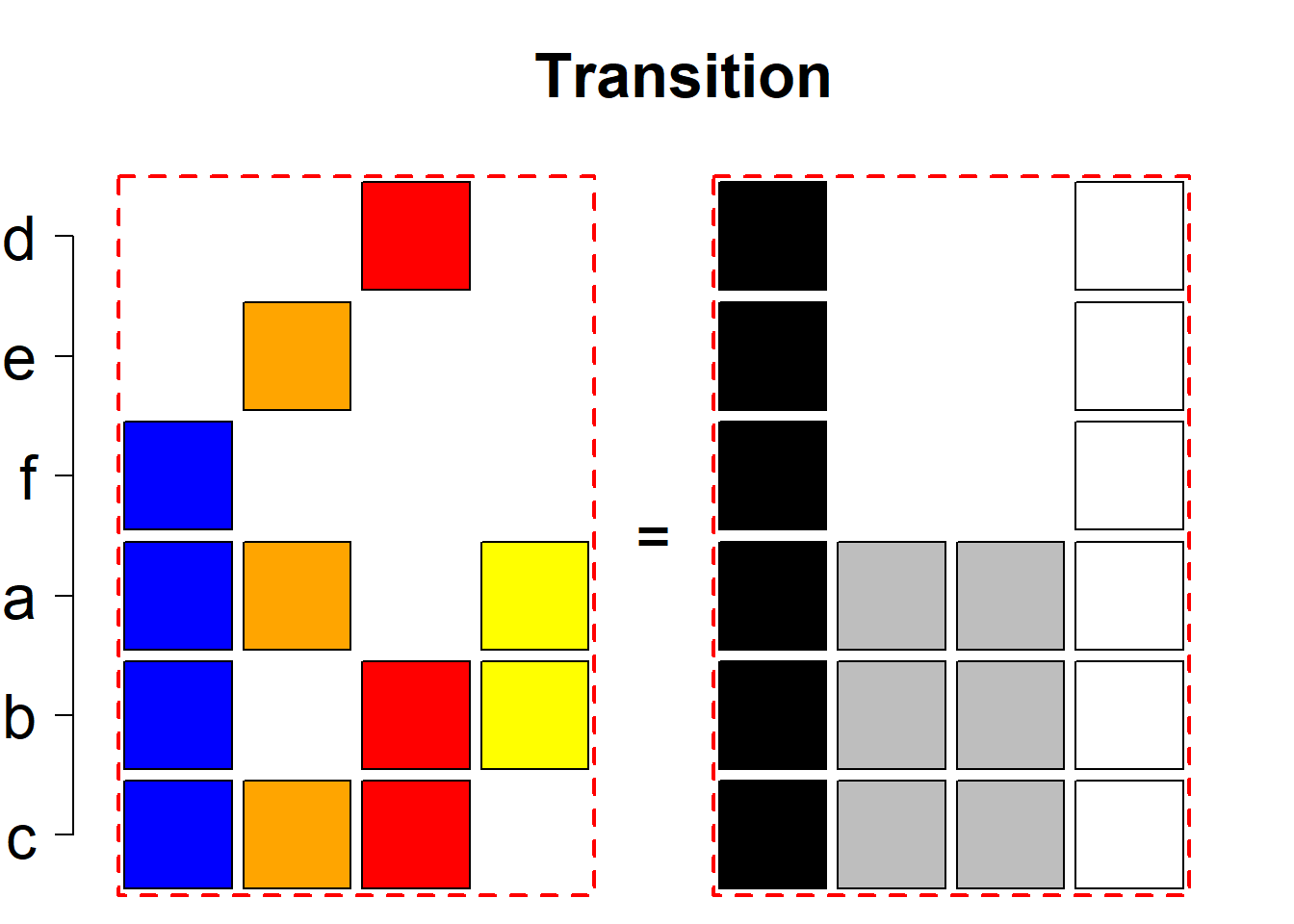
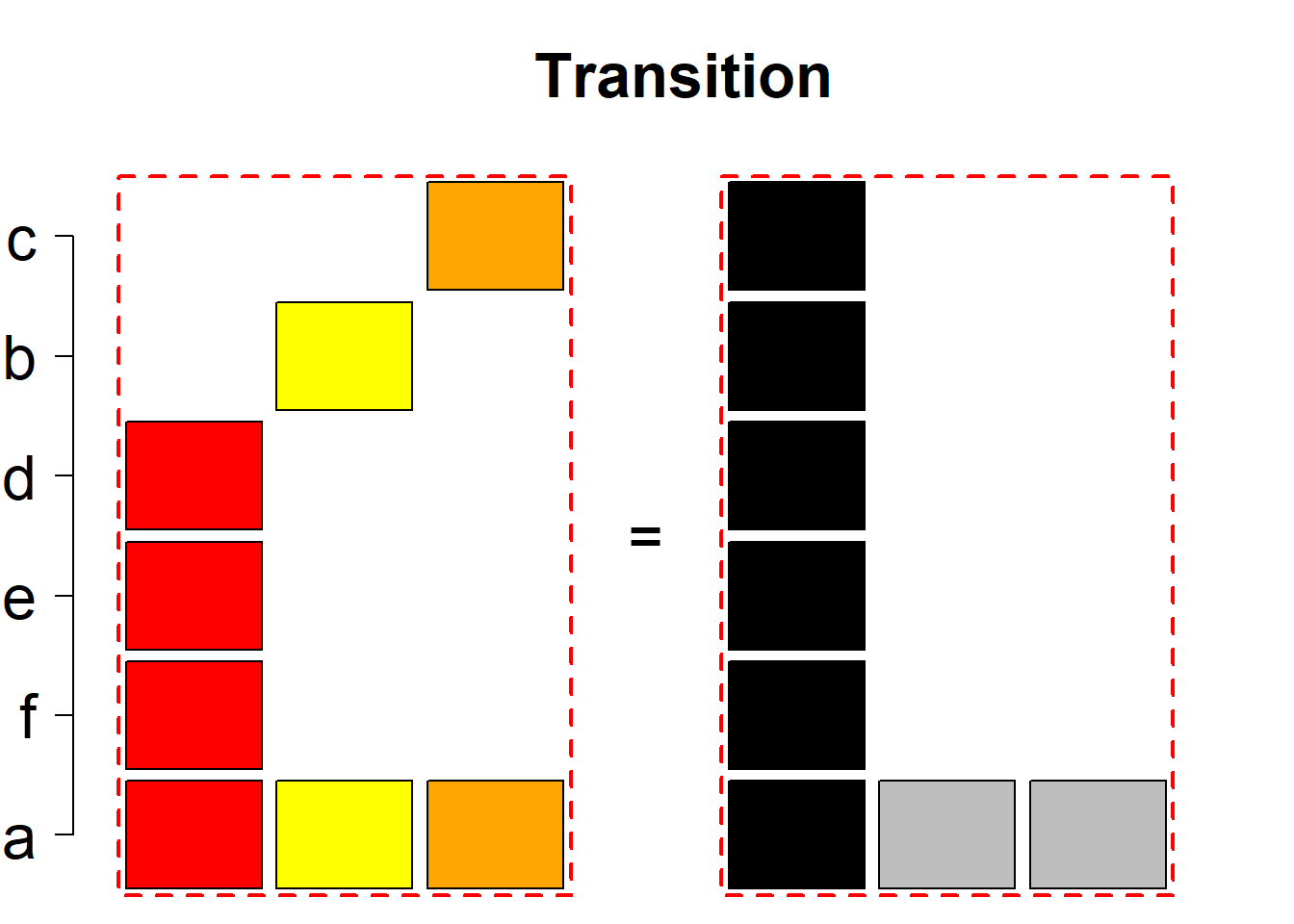
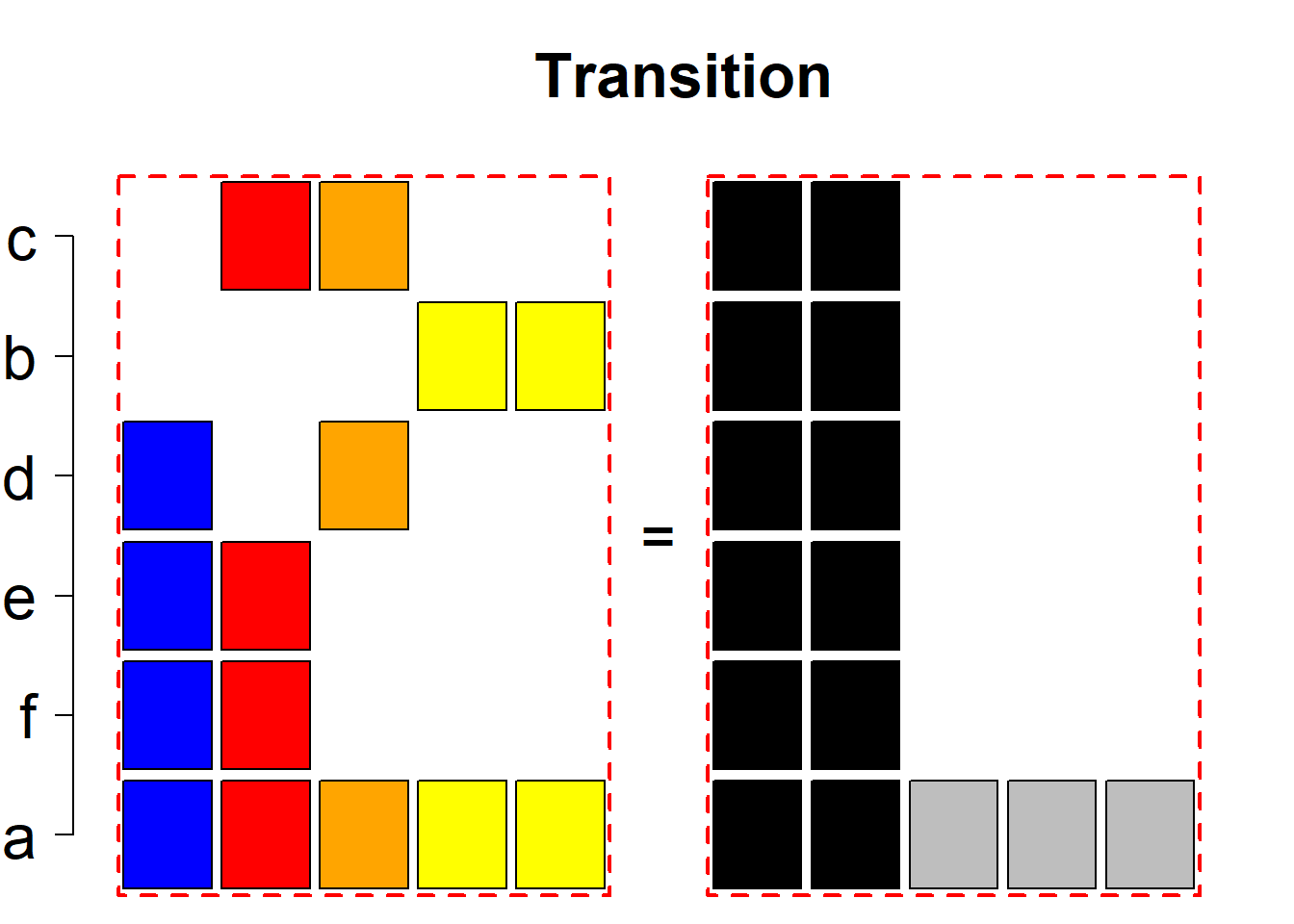
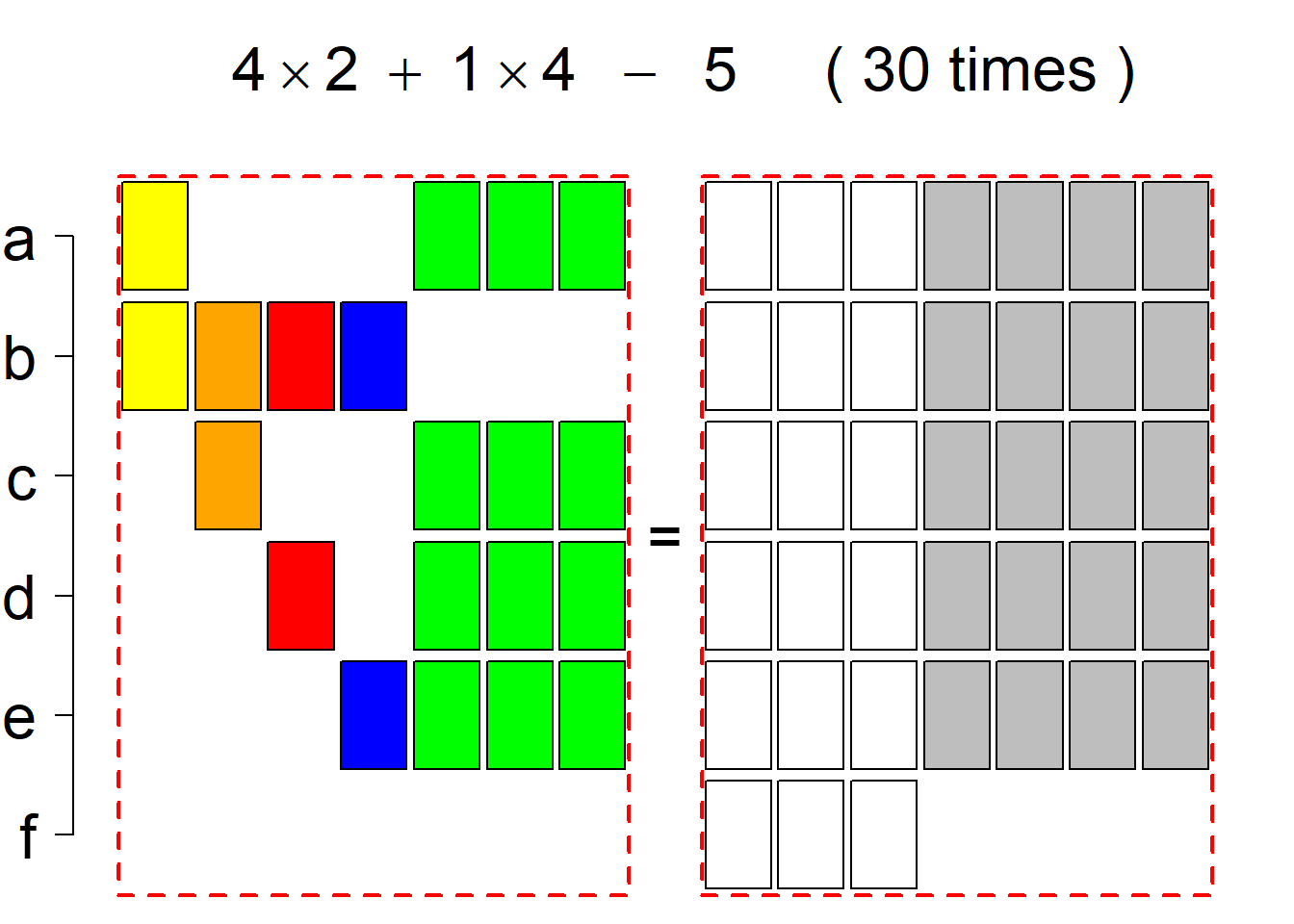
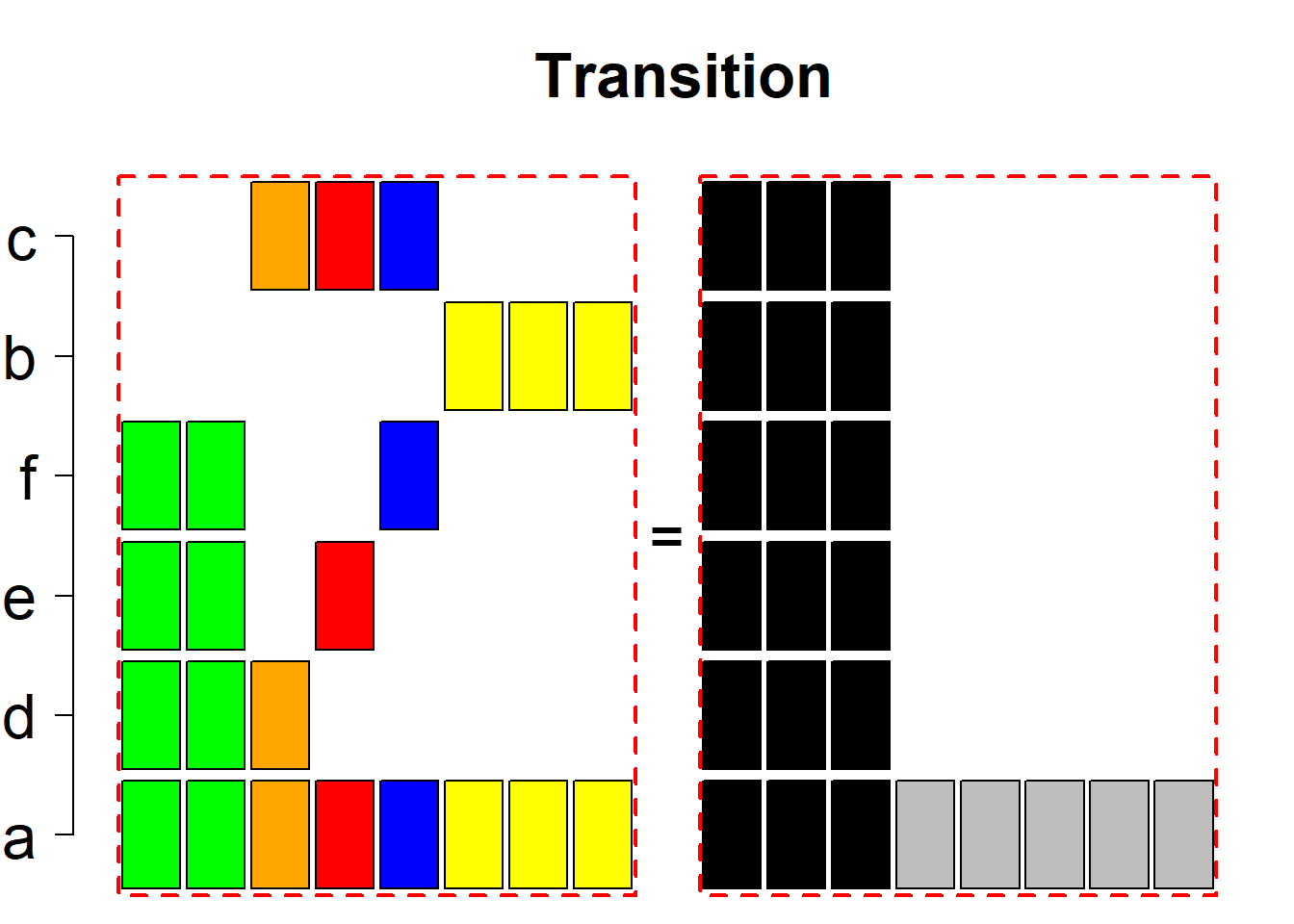
Each hyper-row represents either a pair of mutually complementary permutational types of such systems (in the left and right diagrams) or just one auto-complementary permutational type in the left diagram. By an auto-complementary type is meant the permutational type of such set systems whose complementary systems belong to the same permutational type. The middle diagrams are again auxiliary, describing the transition to the complementary type; in the case of an auto-complementary type it describes the permutational transition from the complementary system back to the set system in the left diagram.